Examen Architecture des Ordinateurs Test 12
EXAMEN ARCHITECTURE DES ORDINATEURS TEST 12
Sujet d'examen CONVERSION, multplixeurs, logique combinatoire, table de verite 20pts
Exercice1 : 10PTS
1) Definir Numération, Algèbre de Boole, fonction booléenne.
2) Dans le schéma ci-contre, associez à chaque numéro le nom du composant correspondant.
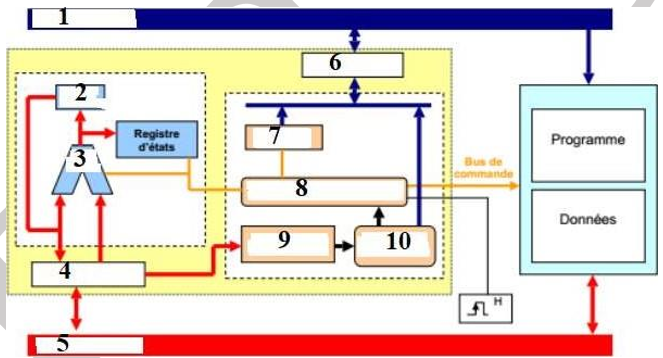
3)Donnez le rôle des éléments 2, 7, 9 et 10.
4) Classer les mémoires suivantes par taille et par rapidité, RAM, registres, disque dures, caches.
5) Quelles sont les opérations réalisables sur dans une mémoire ?
6) Dresser la TV de F1(A,B,C) =\(A \cdot \overline{B} + A \cdot (\overline{B + C}) + \overline{A} \cdot B \cdot \overline{C}\)
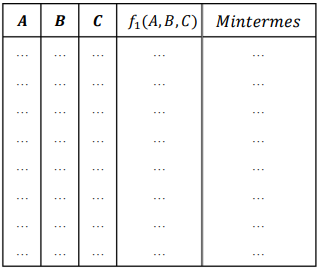
7) Représenter sous la 1 ère forme ( ∑ ∏ ) canonique.
8) Déduire sa représentation de sous la 2 ère forme ( ∏ ∑ ) canonique.
Exercice 2 : Multiplexeurs 5PTS
Soit la figure ci-contre :
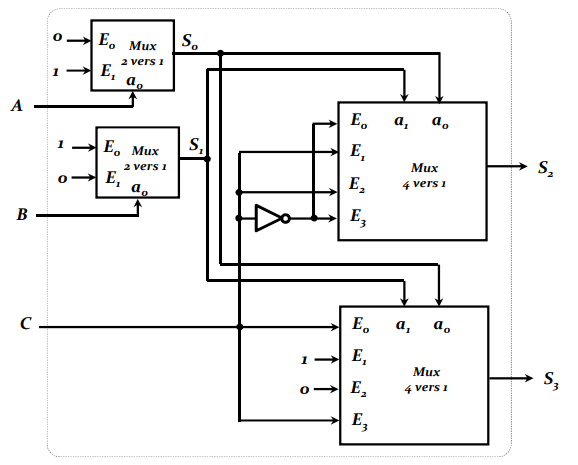
1) Donnez les équations de S0 et S1 .
2) Donnez l’équation de S2 en fonction de A, B, C.
3) Donnez l’équation de S3 en fonction de A, B, C.
4) En réalité S2 et S3 sont des sorties d’un circuit combinatoire, lequel ?
5) Que représentent S2 et S3 dans circuit.
6) Réaliser S2 et S3 à l’aide des Mux à 8 vers 1.
Exercice 3 : 5pts Circuit hidden bit
On considère un circuit logique à k entrées numérotées : a1, a2, …, ak, chacune correspondant à un bit 0 ou 1, et une sortie B, ainsi définie : Pour chaque combinaison des entrées, on calcule la somme s des entrées (en base 10), c’està-dire le nombre d’entrées égales à 1, puis on fait • B = 0 si s = 0 • B = as si 1 ≤ s ≤ k, autrement dit pour toute valeur non nulle de la somme s, on met en sortie B la valeur de l’entrée qui porte ce numéro s.
a) Traiter le cas où k = 1 (une seule entrée a1), en construisant la table de vérité pour en déduire l’équation donnant B.
b) Traiter le cas où k = 2. Simplifier l’équation obtenue à partir de la table de vérité. Constater que l’on obtient pour B le même résultat particulièrement simple que pour k = 1.
c) Cas où k = 3. Construire la table de vérité, avec en colonnes a1, a2, a3, s et B. En déduire l’équation donnant B par rapport aux entrées. Puis utiliser un tableau de Karnaugh pour simplifier cette équation. Dessiner le circuit correspondant.
d) Traiter de la même façon le cas où k = 4, pour aboutir au dessin du circuit après avoir simplifié l’équation.
CORRECTION :
Ajouter un commentaire