EXAMEN ARCHITECTURE DES ORDINATEURS TEST  14

Sujet d'examen dma, Boolr, CONVERSION, multplixeurs, logique combinatoire, table de verite 20pts

Exercice 1 : 4.5PTS

1. A quoi servent les registres suivant du processeur : PC , Registre d’adresse, L’accumulateur.
2. Pourquoi utilise-t-on les mémoires caches ?
3. Classer les mémoires par taille et par rapidité : RAM, registres, disque dur, mémoires cache.
4. Effectuez les conversions suivantes :  (a) 31741₍₈₎ = ( ? )₍₁₆₎ ; (b) 543,5625(10) = ( ? )₍₈₎
5.  Donnez la représentation de 7435,4832 en virgule fixe complément a deux sur 32 bits.

Exercice 2 : Multiplexeurs  6PTS

On désire réaliser le circuit combinatoire permettant d'obtenir le reste r =(r₁r₀)2 de la division par (3)₁₀ d'un nombre X de 4 bits tel que :  (0)₁₀ ≤ X = (X3X2X1X0) ≤ (11)₁₀.

1) Complétez la table de vérité de ce circuit.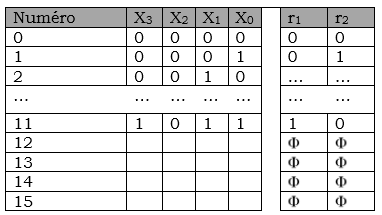

2) Donner les équations simplifiées de r₁ et r₀ .

3) Réaliser ce circuit à l'aide d’opérateurs NAND.

4)Réaliser ce circuit à l'aide de multiplexeurs à 2 entrées et une sortie (et éventuellement d'inverseurs).

Exercice 3 : 5pts Multiplexeurs  Parite d'un Mot

Le but de cet exercice est de concevoir un circuit permettant de détecter la parité d'un mot de 3 bits code sur les entrées E₂, E₁ et E₀. La sortie vaudra 0 si le nombre de « 1 » en entrée est pair (ex : 0011) et 1 sinon (ex : 1000).

1. Completer la table de vérité correspondante a ce circuit.

2) Donner le schema du Circuit.

3) On maintenant construire un circuit combinatoire qui permet de testers parité d'un mot binaire b₃b₂b₁b₀. La sortie vait 1 si le nombre de bits a 1 est paire (par temple, 1001) et 0 sinon (par exemple, 0111)

• Ecrire la table de verite encodant la fonction logique correspondante.
• Utiliser un multiplexeur 16 vers 1 pour realiser cette fonction

Exercice 4 : 4.5pts fonction logique

Soit la fonction logique F donnée par le diagramme suivant :

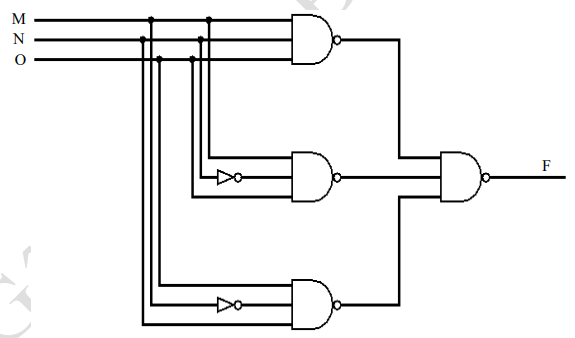
1. Trouver l’expression logique de la fonction F.

2. Simplifier cette expression par la méthode algébrique.

3. Proposer un logigramme plus simple qui donne la fonction F.

EXERCICE

Si vous avez trouvé cet examen corrige de Mr JoëlYk intéressants et utiles, pourquoi ne pas les partager avec d'autres personnes qui pourraient également en bénéficier ? Partagez ce lien sur les réseaux sociaux ou envoyez-le à vos amis et collègues. Vous pourriez aider quelqu'un à améliorer ses compétences en programmation ou à trouver des solutions à des problèmes complexes. N'oubliez pas que la connaissance doit être partagée pour grandir. Merci pour votre soutien et votre partage !

Contact WhatsApp uniquemnet : +237 652027193 | Réaliser Par Joël_Yk

Encore plus d'examen corrige ici !!!