Examen Architecture des Ordinateurs Test 26
EXAMEN ARCHITECTURE DES ORDINATEURS TEST 26
Sujet d'examen CIRCUIT combinatoire, logique combinatoire, codage, complément a 2, sav, sva, numeration, binaire, bit, multiplexeur, forme conjonctive, forme disjonctive, logigramme, table de verité, NAND, ET. 20pts
Exercice 01 : 10pts/ NUMERATION
1) Quel est l’intervalle des entiers codables sur 10 bits en C1 et C2 ?
2. Quel est l'intervalle des entiers représentables en excédent à 128 ? Quelle différence avec le C2 sur 8 bits ?
3. Remplissez le tableau suivant en codant sur un octet
4. Sur un octet en C2 et en excédent 128, effectuer les additions binaires suivantes en ndiquant, le résultat décimal représenté, sa cohérence et le positionnement des indicateurs
Carry et Overflow. 0+0; 1+1; -1+-1; 127+127; -128+-128; 1+-1; 3+-4; 127+-126; 2+-127.
5.Quelles remarques tirez-vous des additions précédentes en C2 et en E128 ? Quelle(s) opération(s) d’ajustement vous semblent nécessaires pour la cohérence des additions binaires en représentation E128 ?
6.En RBNS 8 bits, exprimez la formule de décodage d’un octet b7..b0 en l’entier positif décimal x qu’il représente : x=f(bi).
7.En RBNS 8 bits, exprimez une formule de codage d’un entier positif décimal x en un bit de l'octet b7..b0 qui le représente : bi=g(x).
8.Remplissez le tableau suivant:
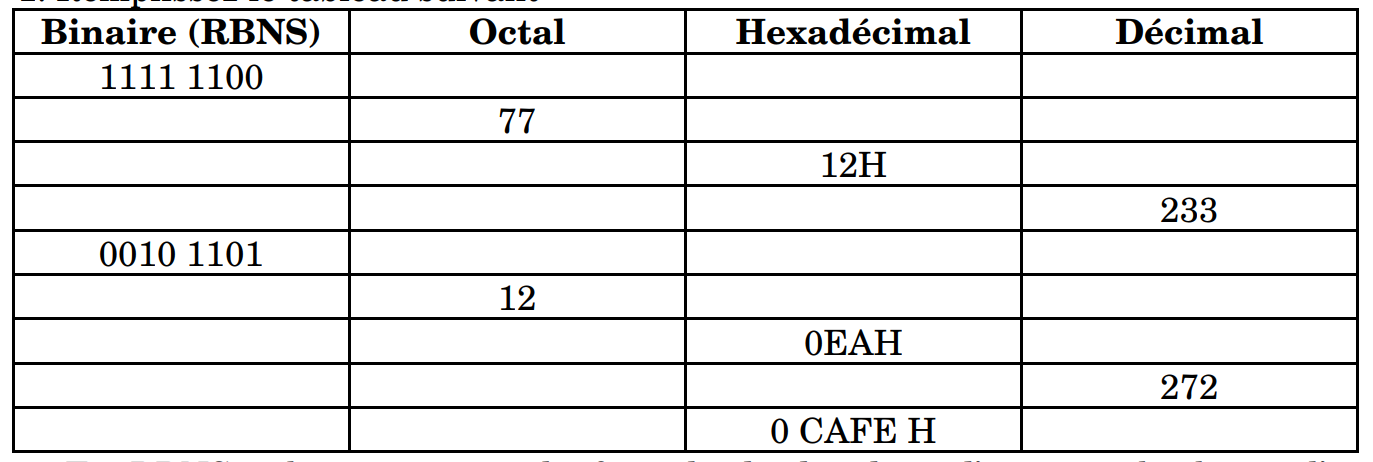9.Remplissez le tableau des additions binaires suivant (additions et résultats).
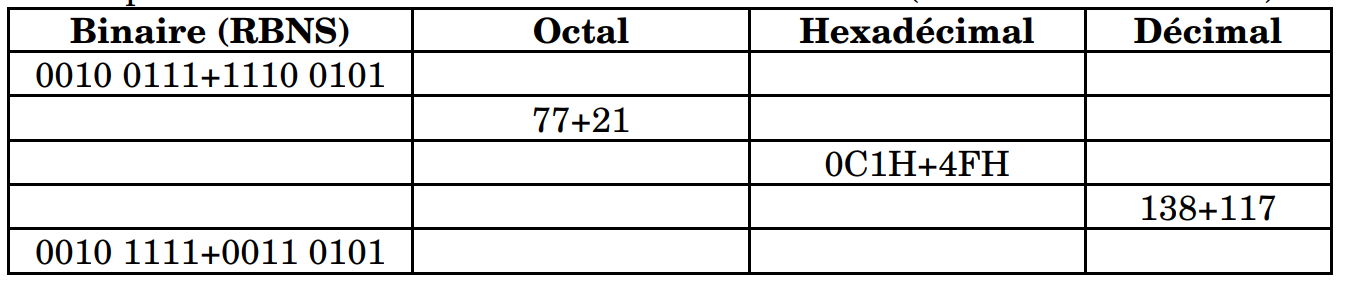
Exercice 2 : 4pts/ Incrémenteur
Une (grande) partie des additions effectuées par un ordinateur consistent simplement a ajouter 1 a une autre valeur x (on incrémente la valeur x).
1. Réaliser un incrémenter 3 bit avec retenue de sortie (Entrées A0A1A2 ; Sorties RI0I1I2).
2. Réaliser aussi le circuit d'un décrémenteur 3 bits, avec « 000 » cas indéfinis (Entrées A0A1A2 ; Sorties D0D1D2).
3. Réaliser la fonction D0 avec un Mux de 3 entrées d’adresses.
4. Réaliser la fonction D1 avec un DEMux de 3 entrées d’adresses.
5. Réaliser la fonction D2 avec un DEMux de 1x4 et un Mux 4x1.
EXERCICE 3 : 4PTS/Rotation
On aime concevoir un circuit qui fait la rotation de 3 bit (CBA) à droite ou à gauche selon la valeur d’une variable en entrée D. Ex : DCBA=0100 => D=0 (rotation à gauche) ; résultat (R0R1R2=001) DCBA=1100 => D=1 (rotation à droite) ; résultat (R0R1R2=010)
1. Donner la table de vérité du circuit.
2. Donner les deux formes canoniques des sorties.
3. Réaliser les trois sorties avec des portes Nand ou Nor seulement.
EXERCICE 4 : Encodeur 3 bits
Un encodeur n bits est un circuit à 2^n entrées (mutuellement exclusives) et n sorties qui permet d’encoder le numéro de la ligne d’entrée activée en binaire. Par exemple, si la 6e ligne d’un encodeur 3 bits est activée, alors les sorties seront A=1 B=0et C=1.
Questions :
- Quelle est la particularité de ce circuit ?
- Comment détecter une combinaison d’entrées invalide ?
- Écrire une table de vérité pour l’encodeur 2 bits.
- Réaliser le circuit correspondant.
CORRECTION :
Ajouter un commentaire