Sujet d'Examen ALGORITHMIQUE AVANCÉS & COMPLEXITÉ

Question de mise en confiance

Quelle est la différence entre un problème accepté par machine de Turing et un problème décidé par machine de Turing?

Exercice 1: Algorithmes de graphe et Complexité

1- On veut montrer qu'un arbre rouge et noir ayant n nœuds internes à une hauteur au plus égale à 2 x log(n+1):

a) Montrer que, pour un nœud x quelconque dans un arbre rouge et noir, le sous-arbre enraciné en x contient au moins (2^H_n(x)-1) nœuds internes. H_n(x) est la hauteur noire du nœud x.
b) Déduire de la question (a) la hauteur d'un arbre rouge et noir comportant n nœuds internes.

2- Soit G = (S, A) un graphe, un sous-ensemble des sommets de G est stable s'il ne contient pas de paire de sommets adjacents. Montrez que tout sous-ensemble d'un ensemble stable est stable.

3- Déduire de l'item 2 que c'est la même chose de se donner un k-coloriage d'un graphe, que de le partitionner en k sous-ensembles stables.

4- Soit G un graphe non orienté, montrez qu'au moins un des deux graphes, G ou son complémentaire, est connexe.

5- Quelle est le nombre chromatique d'un graphe bipartite? Démontrez votre affirmation.

6- Utilisez la théorie des graphes pour démontrer que parmi un ensemble de n amis, il y a au moins deux amis qui ont le même nombre d'amis.

Exercice 2: NP-Complétude et Programmation dynamique

1- Qu'est-ce qu'un problème NP-complet? Quelle est la procédure pour démontrer qu'un problème est NP-complet?

2-Énoncez le problème SAT et démontrez qu'il est NP-complet.

3- Choisissez un autre problème NP-Complet de votre choix et montrez la réduction en temps polynomiale de ce problème avec SAT.

4- Quelles sont les conditions permettant de dire qu'un problème est un problème de programmation dynamique?

5- Quand dit-on qu'un problème de programmation dynamique est de la classe monadique serial? Donnez un exemple !

6- Énoncez le problème de parenthésage optimal d'une chaîne de matrices (Matrix Chain Ordering Problem) et montrez que c'est un problème de programmation dynamique. Quelle est la classe de ce problème?

7- Montrez que le problème de recherche du plus long chemin dans un graphe n'est pas un problème de programmation dynamique.

CORRECTION : COMPLEXITE ET ALGORITHME AVANCE

Par : Mr Joël_yk

Questions mise en confiance :

Indécidabilité d'un problème ≡ il n'existe pas d'algorithme résolvant ce problème de manière générale ≡ il n'existe pas de machine de Turing qui prend en entrée les données (Pb) et qui s'arrête toujours en donnant une solution. Exemple : Le problème de l'arrêt pour les machines de Turing est indécidable. Un Pb accepté par une machine de Turing est dit Turing-acceptable ou récursivement énumérable. Si la machine de Turing s'arrête sur toutes les entrées possibles (c-à-d pour tous les informations i, i ∈ P ou i ∉ P), alors il est dit Turing-décidable ou récursif.

Exercice 1 : Algorithmes de Graphe et Complexité

(a) On peut prouver cette proposition par induction sur la hauteur de x. Si la hauteur de x est 0, x est une feuille et le sous-arbre enraciné a x contient 0 nœud interne, c’est-à-dire 2^Hn(x) − 1 = 2^0 − 1. Soit x un nœud de hauteur h(x) > 0. Ce nœud a deux fils, g et d. Dans ce cas, Hn(g) ≥ Hn(x) − 1 et Hn(d) ≥ Hn(x) − 1. De plus, la hauteur de g et de d est inférieure à la hauteur de x, donc, en appliquant l’hypothèse d’induction à g et d, les sous-arbres enracinés à g et d possèdent chacun au moins 2^Hn(g) − 1 ≥ 2^Hn(x) − 1 − 1 et 2^Hn(d) − 1 ≥ 2^Hn(x) − 1 − 1 nœuds internes. Il s’ensuit que le sous-arbre enraciné à x possède au moins : 2 × (2^Hn(x) − 1 − 1) + 1 = 2^Hn(x) − 1 nœuds internes.

(b) Soit h la hauteur de l’arbre. D’après la propriété 3 (Si un nœud est rouge, alors ses deux fils sont noirs), au moins la moitié des nœuds d’un chemin simple reliant la racine de l’arbre à une feuille doivent être noirs (preuve facile par l’absurde). En conséquence, la hauteur noire de la racine vaut au moins h/2, donc n ≥ 2^(h/2) − 1, d’où h ≤ 2 × log(n + 1).

Soit G = (S, A) un graphe, un sous-ensemble des sommets de G est stable s’il ne contient pas de paire de sommets adjacents. Montrer que tout sous-ensemble d’un ensemble stable est stable. Réponse : Soient G = (S, A) un graphe, avec S l'ensemble de sommets et A l'ensemble des arêtes, et soit S' un sous-ensemble stable de S, c'est-à-dire un sous-ensemble tel que pour tout u, v dans S', il n'existe pas de (u, v) dans A. Nous allons démontrer que pour tout sous-ensemble T de S', T est également stable. Notons que T peut être défini comme T = {x dans S' | x appartient à T}. Soient u et v deux éléments de T, alors u et v sont également des éléments de S', donc (u, v) n'appartient pas à A. Par conséquent, nous pouvons démontrer que T est également stable. En utilisant la définition formelle, nous pouvons écrire cette démonstration de la manière suivante : Soit T un sous-ensemble de S', alors pour tout u, v dans T, nous avons (u, v) ∉ A, car S' est stable et u, v ∈ S'. Cela montre que la stabilité est une propriété transitive pour les sous-ensembles d'un graphe G, ce qui signifie que si un sous-ensemble est stable, alors tous ses sous-ensembles sont également stables.

3) Supposons que nous ayons un k-coloriage valide pour un graphe G, c'est-à-dire que chaque sommet est colorié avec l'une des k couleurs de telle sorte que deux sommets adjacents n'aient pas la même couleur. Nous pouvons alors construire k sous-ensembles stables à partir de ces couleurs de la manière suivante :

1-Pour chaque couleur i de 1 à k, créez un sous-ensemble stable Si contenant tous les sommets coloriés avec la couleur i.

2-Puisque deux sommets ayant la même couleur ne sont pas adjacents (selon la règle du k-coloriage), chaque sous-ensemble S_i est stable.

3-Nous avons maintenant k sous-ensembles stables S₁, S₂, ..., S_k qui partitionnent l'ensemble de sommets S de G. Cela démontre que le k-coloriage d'un graphe peut être utilisé pour partitionner le graphe en k sous-ensembles stables.

Oui observer aussi que L'inverse est également vrai. Si vous avez une partition du graphe en k sous-ensembles stables, vous pouvez attribuer une couleur différente à chaque ensemble stable pour obtenir un k-coloriage valide. Cette correspondance montre que se donner un k-coloriage d'un graphe est équivalent à le partitionner en k sous-ensembles stables.

4) Soit G un graphe non orienté, montrez qu’au moins un des deux graphes, G ou son complémentaire, est connexe. Réponse : Soit G = (S, A) un graphe non orienté, avec S l'ensemble de sommets et A l'ensemble des arêtes. Le complémentaire de G, noté G', est un graphe (S, A') tel que A' = {(u, v) | (u, v) n'appartient pas à A et u, v dans S}. Nous allons démontrer que, pour un graphe non orienté G, soit G est connexe, soit son complémentaire G' est connexe. Supposons que G n'est pas connexe, c'est-à-dire qu'il existe un sous-ensemble S' de sommets tels que pour tout u dans S', il n'existe pas de chemin de u à un autre sommet v dans S \ S'. Alors, pour tout (u, v) avec u dans S' et v dans S \ S', (u, v) appartient à A', car (u, v) n'appartient pas à A. Par conséquent, tous les sommets de S' sont connectés entre eux par des arêtes dans A', ce qui signifie que G' est connexe. En utilisant la définition formelle, nous pouvons écrire cette démonstration de la manière suivante : Soit G = (S, A) un graphe non orienté. Soit G' = (S, A') son complémentaire. Alors, soit G est connexe, soit G' est connexe. Supposons que G n'est pas connexe, c'est-à-dire qu'il existe un sous-ensemble S' de sommets tels que pour tout u dans S', il n'existe pas de chemin de u à un autre sommet v dans S \ S'. Alors, pour tout (u, v) avec u dans S' et v dans S \ S', (u, v) appartient à A', ce qui signifie que G' est connexe.

5) Supposons un graphe bipartite G = (S, A). Alors S peut être partitionné en deux ensembles disjoints S1, et S2 tels que chaque arête de G relie un sommet de S1 et un sommet de S2. Attribuons la première couleur à chaque sommet dans S1 et la deuxième couleur à chaque sommet dans S2. Puisque G est bipartite, aucune arête de G ne relie deux sommets appartenant au même ensemble. Cela signifie que deux sommets adjacents ne peuvent pas avoir la même couleur. Par conséquent, G est 2-chromatique.

6) Utilisons la théorie des Graphes : Considérons le graphe dont les sommets sont les n amis (personnes) du groupe Genius. On suppose bien entendu, que la relation d’amitié est une relation symétrique. Deux sommets du graphe sont reliés par une arête lorsque les deux personnes correspondantes sont amies. Il suffit alors de prouver que deux sommets au moins de ce graphe ont même degré. Supposons que les n sommets soient tous de degré distinct. On peut alors numéroter les sommets de x₀à x_n avec : 0 ≤ d(x₀) < d(x₁) < ⋯ < d(x_(n-1)). Or le degré maximal d’un sommet d’un graphe simple d’ordre n est égal à n-1. On a donc nécessairement d(x_i) = i de {0,1,…,n-1}. Avec notre hypothèse, le graphe comprendrait un sommet de degré 0 (C’est une personne bien seule …) et un sommet de degré n-1, donc relié à tous les autres sommets du graphe, en particulier au sommet isolé, ce qui est contradictoire. Nous avons donc montré qu’un graphe simple contient au moins deux sommets de même degré. Ainsi, parmi un ensemble de n amis, il y a au moins deux amis qui ont le même nombre d’amis.

Exercice 2 : NP COMPLETUDE & Programmation Dynamique

1) Les problèmes de la classe NP-complet sont des problèmes NP qui ne peuvent être résolus en un temps polynomial, mais pour lesquels tout autre problème NP peut être réduit à eux. Cela signifie que si une solution efficiente (en un temps polynomial) était trouvée pour un problème NP-complet, alors des solutions efficientes pourraient également être trouvées pour tous les autres problèmes NP.

2) Énonce : Une instance de SAT est une formule booléenne f composée de :

n variables booléennes : x₁, x₂, ..., x_n ;
m connecteurs booléens : toute fonction booléenne avec une ou deux entrées et une sortie, telle que ∧ (ET), ∨ (OU), ¬ (NON), → (implication), ↔ (si et seulement si) ; et
Des parenthèses. (Sans nuire à la généralité, on suppose qu’il n’y a pas de parenthèses redondantes, c’est-à-dire qu’il y a au plus une paire de parenthèses par connecteur booléen.)

Il est facile d’écrire une formule booléenne f dans une longueur qui est polynomiale en n + m. Comme c’est le cas avec les circuits combinatoires booléens, une assignation de vérité pour une formule booléenne f est un ensemble de valeurs pour les variables de f, et une assignation satisfaisante est une assignation pour laquelle l’évaluation de la formule donne 1. Une formule possédant une assignation satisfaisante est une formule satisfaisable. Le problème de la satisfiabilité consiste à savoir si une formule booléenne donnée est satisfaisable ; en termes des langages formels, on dira : SAT = {〈ϕ〉 tel que est une formule booléenne satisfaisable}

Bien soit la formule ϕ = (( x₁ → x₂) ∨ ¬((¬x₁ ↔ x₃) ∨ x₄)) ∧ ¬ x₂ elle possède l’assignation satisfaisante 〈x₁ = 0, x₂ = 0, x₃ = 1, x₄ = 1〉, puisque

ϕ = ((0 → 0) ∨ ¬((¬0 ↔ 1) ∨ 1)) ∧ ¬0
   = (1 ∨ ¬(1 ∨ 1)) ∧ 1
   = (1 ∨ 0) ∧ 1 = 1

Et on conclut que cette formule ϕ appartient à SAT.

Fin de l’énoncé (je vous l’accorde c’est très long mais facile à comprendre, vrai de vrai !)

Maintenant démontrons qu’il est NP-Complet :

Soit la formule booléenne suivante (¬x₁ ∨ x₂ ∨ x₃) ∧ (¬x₂ ∨ x₃) ∧ (¬x₃ ∨ x₁) Pour x₁=0, x₂=1, x₃=1 la formule est satisfaisable, c’est-à-dire admet un modèle. L’algorithme naïf permettant de déterminer si une formule booléenne arbitraire est satisfaisable ne s’exécute pas en temps polynomial. Il existe 2ⁿ assignations possibles d’une formule ϕ à n variables. Si la longueur de f est polynomiale en n, alors la vérification de chaque assignation demande un temps Ω(2ⁿ), ce qui est suprapolynomial par rapport à la longueur de ϕ. Comme nous allons le montrer, un algorithme polynomial a très peu de chances d’exister. Pour montrer que la satisfiabilité d’une formule booléenne est un problème NP-Complet, nous allons :

Montrer que SAT ∈ NP : On montre qu’un certificat consistant en une assignation satisfaisante pour une formule f en entrée peut être validé en temps polynomial. L’algorithme de vérification remplace tout simplement chaque variable de la formule par sa valeur correspondante, puis évalue l’expression. Ce travail peut facilement s’effectuer en temps polynomial. Si l’expression a pour évaluation 1, la formule est satisfaisable. Donc, SAT ∈ NP.
Montrer que SAT est NP-difficile : On montre que CIRCUIT-SAT ≤_P SAT. Autrement dit, toute instance du problème de satisfiabilité de circuit peut être réduite en temps polynomial à une instance du problème de satisfiabilité de formule. On peut faire appel à une récurrence pour exprimer un circuit combinatoire booléen quelconque comme une formule booléenne. On regarde simplement la porte qui produit le résultat du circuit, et on exprime de manière récurrente chacune des entrées de la porte en tant que formules. La formule correspondant au circuit est alors obtenue en écrivant une expression qui applique la fonction de la porte aux formules de ses entrées. Malheureusement, cette méthode directe n’est pas une réduction en temps polynomial. Les sous-formules partagées peuvent faire croître exponentiellement la taille de la formule générée, pour peu qu’il y ait des portes dont les fils de sortie aient des facteurs d’éventail de 2 ou plus. Donc, l’algorithme de réduction devra être un peu plus astucieux.

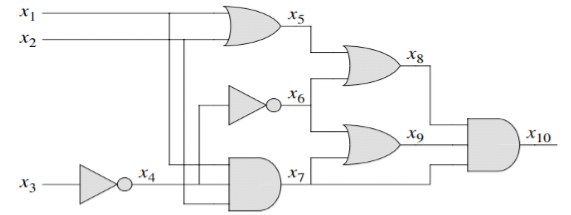
A partir du schéma ci-dessus, on dénote le principe fondamental de la réduction de CIRCUIT-SAT à SAT. Pour chaque fil x_i du circuit C, la formule ϕ à une variable x_i. L’opération propre à une porte peut maintenant être exprimée comme une formule mettant en jeu les variables situées de ses fils incidents. Par exemple, l’opération de la porte ET en sortie est x₁₀ ↔ (x₇ ∧ x₈ ∧ x₉). La formule ϕ produite par l’algorithme de réduction est le ET entre la variable de sortie du circuit et la conjonction des clauses décrivant l’opération de chaque porte. Pour le circuit de la figure 4, la formule est :

ϕ = x₁₀ ∧ (x₄ ↔ ¬x₃) ∧ (x₅ ↔ (x₁ ∨ x₂)) ∧ (x₆ ↔ ¬x₄) ∧ (x₇ ↔ (x₁ ∧ x₂ ∧ x₄)) ∧ (x₈ ↔ (x₅ ∨ x₆)) ∧ (x₉ ↔ (x₆ ∧ x₇)) ∧ (x₁₀ ↔ (x₈ ∧ x₉))

Étant donné un circuit C, il est immédiat de produire une telle formule f en temps polynomial. Pourquoi le circuit C est-il satisfaisable exactement quand la formule f est satisfaisable ? Si C possède une assignation satisfaisante, chaque fil du circuit a une valeur bien définie et la sortie du circuit est 1. Donc, l’assignation de valeurs de fil aux variables de f fait que chaque clause de f est évaluée à 1, et donc que leur conjonction est aussi évaluée à 1. Réciproquement, s’il existe une assignation qui donne une évaluation 1 pour f, le circuit C est satisfaisable de par une démonstration analogue. On a donc montré que CIRCUIT-SAT ≤_P SAT.

Donc SAT est un problème NP-Complet.

3. Problème de Clique

Une clique dans un graphe non orienté G = (S, A) est un sous-graphe complet de G, c’est-à-dire que deux sommets quelconques de la clique sont toujours adjacents. La taille d’une clique est le nombre de sommets qu’elle contient. Le problème de la clique est le problème d’optimisation consistant à trouver une clique de taille maximale dans un graphe. Le problème de décision associé est celui de savoir s’il existe une clique de taille K dans le graphe. De manière formelle la définition d’une clique est :

CILIQUE = { < G, k > / G est un graphe contenant une Clique de taille k }

En entrée : Graphe G = (S, A) et une constante k
Sortie : Existe-t-il dans G une clique S’ ⊆ S avec |S’| = k ?

* Montrons que clique appartient à NP : Pour montrer que CILIQUE ∈ NP, pour un graphe donné G = (S, A), on utilise l’ensemble S’ ⊆ S des sommets de la clique comme certificat pour G. Vérifier que S’ est une clique peut être accompli en temps polynomial, en testant si pour toute paire u, v ∈ S’ l’arête (u, v) appartient à A.

** Nous allons montrer que 3-CNF-SAT se réduit polynomialement à CLIQUE, c’est-à-dire 3-CNF-SAT ≤_P CLIQUE. L’algorithme de réduction commence avec une instance de 3-CNF-SAT. Soit f = ( C₁∧ C₂ ∧ .... C_k)une formule booléenne sous forme 3-CNF à k clauses. Pour r = 1, 2, ..., k, chaque clause C_r possède exactement trois littéraux distincts l_r1, l_r2 et l_r3. Nous allons construire un graphe G tel que f soit satisfaisable si et seulement si G possède une clique de taille k. Le graphe G = (S, A) est construit de la manière suivante. Pour chaque clause C_r = ( l_r1∨ l_r2 ∨ l_r3) de f, on place un triplé de sommets v_r1, v_r2 et v_r3 dans S. On place une arête entre deux sommets v_ri et v_sj si les deux conditions suivantes sont satisfaites :

v_ri et v_sj sont dans des triplets différents, autrement dit si r est différent de s ;
Leurs littéraux correspondants sont cohérents, autrement dit l_ri n’est pas la négation de l_sj.

Ce graphe peut se calculer facilement à partir de f en temps polynomial. À titre d’exemple de cette construction, si l’on se donne f = (x₁ ∨ ¬x₂ ∨ ¬x₃) ∧ (x₂ ∨ ¬x₁ ∨ x₃) ∧ (x₁ ∨ x₂ ∨ x₃) alors G est le graphe représenté à la figure suivante.

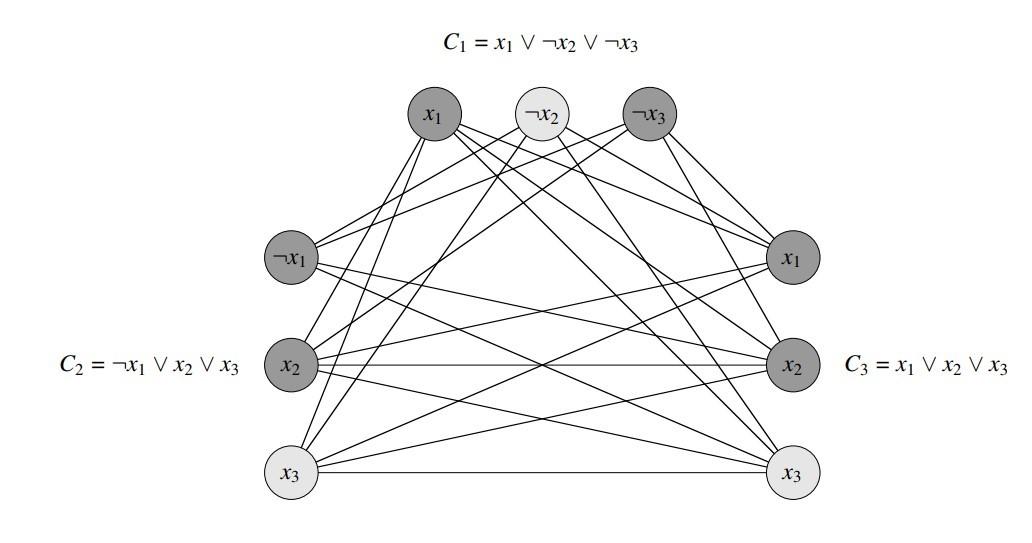
Graphe de la formule

f= (x₁∨ ¬x₂∨ ¬x₃) ∧ (¬x₁∨x₂∨x₃) ∧ (x₁∨x₂∨x₃)

Voici mon astuce : Si tu observes bien le schéma tu verras qu’un élément n’est pas relie à son complément et les éléments de même clause ne sont pas relie entre eux attention à ce détaille. (Source PandaCodeur.com)

Montrons que ce passage de f à G est une réduction.

D’abord, supposons que f est une assignation satisfaisante. Alors, chaque clause C_r contient au moins un littéral l_ri ayant la valeur 1, et chaque littéral de ce type correspond à un sommet v_ri. En prenant l’un de ces littéraux ayant la valeur vraie dans chaque clause, on obtient un ensemble S de k sommets. Nous affirmons que S est une clique. Pour deux sommets quelconques v_ri, v_sj ∈ S, où r ≠ s, l’assignation satisfaisante associe la valeur 1 aux deux littéraux l_ri et l_sj correspondants, et les littéraux ne peuvent donc pas être compléments. Donc, d’après la construction de G, l’arête (v_ri, v_sj) appartient à A. Le graphe précédent issu de la formule 3-CNF f = C₁ ∧ C₂ ∧ C₃, où C₁ = (x₁ ∨ ¬x₂ ∨ ¬x₃), C₂ = (¬x₁ ∨ x₂ ∨ x₃) et C₃ = (x₁ ∨ x₂ ∨ x₃), lors de la réduction de 3-CNF-SAT à CLIQUE. L’assignation < x₁ = 0 ou 1, x₂ = 0, x₃ = 1 > est satisfaisante. Cette assignation vérifie C₁ avec ¬x₂ et vérifie C₂ et C₃ avec x₃, ce qui correspond à la clique dont les sommets sont en clair.

Supposons maintenant que G contienne une clique de taille k. Comme les littéraux d'une même clause ne sont pas reliés, cette clique contient un littéral exactement dans chaque clause. Montrons alors qu'il existe une assignation qui rend tous ces littéraux vrais. Chaque littéral de cette clique est égal à x_i ou à ¬x_i. Pour que ce littéral soit vrai, on impose la valeur 1 ou 0 à la variable correspondante x_i. Comme tous les littéraux de la clique sont reliés par une arête, ils ne sont pas contradictoires deux à deux. Ceci signifie que deux littéraux quelconques de la clique concernent deux variables distinctes x_i et x_j avec i ≠ j ou alors ils concernent la même variable x_i mais ils imposent la même valeur à la variable x_i. On obtient alors une assignation cohérente des variables apparaissant dans la clique. En affectant n'importe quelle valeur à chacune des autres variables, on obtient une affectation qui donne la valeur 1 à la formule f.

En conclusion : 3-SAT ≤_P CLIQUE.

4) Réponse : La programmation dynamique permet de résoudre des problèmes respectant deux critères : le critère d’optimalité et le critère de chevauchement de sous-structures.

5) Classe non-sérielle et classe monadique

La classe non-sérielle est constituée des problèmes de programmation dynamique pour lesquels la solution d’un sous-problème à un niveau N donné dépend des solutions des sous-problèmes de plusieurs niveaux précédents (inférieurs à N).

La classe monadique est constituée des problèmes de programmation dynamique pour lesquels le nombre de termes récursifs est égal à un. Exemple : Le problème de LCS appartient à la classe monadique. En effet, dans l’équation fonctionnelle qui décrit sa solution, la fonction de composition ne contient qu’un seul terme récursif. Dans toutes les alternatives du membre droit de cette équation, l’évaluation du sous-problème L(i,j) ne dépend que d’un seul sous-problème (terme récursif) à la fois : soit L(i−1,j−1)+1, soit L(i,j−1), soit L(i−1,j).

6) Énoncé du problème d’ordonnancement d’une chaîne de multiplication de matrices (MCOP)

Le problème d'ordonnancement de chaîne de multiplication de matrices consiste à déterminer l'ordre optimal dans lequel les matrices d'une chaîne doivent être multipliées pour minimiser le nombre total de multiplications scalaires effectuées. (En gros le nombre de parenthèses possibles d’une expression à n termes est exponentielle en n.)

Démonstration que le problème MCOP est un problème de programmation dynamique

Étapes après étapes

Structure d’une Solution Optimale :
n = 6 => A₁ * A₂ * A₃ * A₄ * A₅ * A₆ ?

Supposons (((A₁ * A₂) * A₃) * A₄) * (A₅ * A₆) Optimale.

Alors (((A₁ * A₂) * A₃) * A₄) est Optimal pour A₁ * ... * A₄

<< Tout sous-chemin d’un plus court chemin est un plus court chemin >>

Sous-Problème : est un Problème restreint aux Produits A_i * ... * A_j

Décomposition : (A₁ * A₂ * A₃ * A₄)

On peut donc pour ce problème dynamique avoir un graphe Acyclique :

Pour tout i ≤ k ≤ j

Équation de Bellman :

f(i, j) : Nombre minimal de multiplications pour les produits A_i * ... * A_j
f(i, j) = min_{i ≤ k ≤ j} (f(i, k) + f(k+1, j) + m_{i-1} * m_k * m_j)
∀ i = 1...n-1, ∀ j = i+1...n
f(i, i) = 0 ∀ i = 1...n

7) Recherche du plus long chemin dans un graphe

La recherche du plus long chemin dans un graphe n’est pas un problème de Programmation Dynamique : Étant donné un graphe cyclique dirigé pondéré (DAG) et un sommet S qu’il contient, trouver les distances les plus longues entre S et tous les autres sommets du graphe donne 1. Le problème du chemin le plus long pour un graphe n’est pas aussi simple que le problème du chemin le plus court car le problème du chemin le plus long n’a pas de propriété de sous-structure optimale.

★ ★ ★ ★ ★

Aucune note. Soyez le premier à attribuer une note !

Ajouter un commentaire

Nom

E-mail

Site Internet

Anti-spam