Exercice 1 : Calcul des complexités (6 pts)

1.Utiliser un arbre récursif pour déterminer une bonne borne supérieure asymptotique pour la récurrence :

$$ T(n) = 3T\left(\frac{n}{2}\right) + n $$

2.Vérifier la réponse à l'aide de la méthode par substitution.

Considérons un algorithme qui effectue une recherche linéaire dans une liste non triée de taille \( n \) pour trouver un élément spécifique. La recherche s'arrête dès que l'élément est trouvé.

3.Déterminez la complexité temporelle de cet algorithme dans le pire des cas.

4.Expliquez comment la complexité temporelle pourrait être améliorée si la liste était triée.

L'algorithme d'exponentiation rapide est basé sur la remarque suivante :

Pour calculer \( a^2 \), il suffit de savoir calculer \( a \) et de faire une multiplication, et pour calculer \( a^{2p+1} \), il suffit de savoir calculer \( a^p \) et de faire deux multiplications.

5.Démontrer que, pour tout \( n \geq 1 \), il est possible d'écrire une fonction exporapide(a, n) pour laquelle le nombre total de multiplications effectuées par un appel est inférieur ou égal à :

$$ 2 + 2 \log_2(n) $$

Exercice 2 : Algorithmes gloutons

Supposons que vous ayez un ensemble de tâches à effectuer, chaque tâche ayant une durée d'exécution et une date limite. L'objectif est de maximiser le nombre de tâches réalisées tout en respectant les dates limites.

1.Proposez un algorithme glouton pour résoudre ce problème.

2.Démontrez la validité de l'algorithme en montrant qu'il maximise effectivement le nombre de tâches réalisées.

Exercice 3 : Arbres couvrant de coût minimum

Appliquer l'algorithme de Prim pour trouver l'arbre couvrant de coût minimum.

Exercice 4 : Graphes et recherche de plus courts chemins

La communauté urbaine de PandaVille est constituée de 07 villes : Douala, Bafoussam, Bertoua, Garoua, Ebolowa, Limbe et Maroua. Les trois premières villes sont séparées des quatre autres par le fleuve Sanaga, dont la largeur maximale de 300 km sépare Bertoua et Maroua ; sa largeur minimale est de 25 km entre Douala et Garoua. Pour des raisons socio-économiques, les autorités de Yaoundéville, dont la "capitale" est Douala, voudraient mieux connaître le réseau routier actuel afin de prendre des décisions stratégiques par la suite.

L'ensemble des routes de la communauté est présenté à l'aide du tableau ci-dessous :

Après avoir recensé ces données, les autorités font appel à votre expertise pour répondre à cette série de questions (vous devez y répondre en vous servant des outils mathématiques de la théorie des graphes vus en cours) :

1. En étant dans n'importe quelle ville de la communauté, est-il possible de se rendre dans n'importe quelle autre ville ? Justifiez votre réponse à l'aide d'une démonstration formelle.
2. Si non, quelle(s) route(s) (de distance(s) minimale(s)) faut-il construire pour pouvoir partir de n'importe quelle ville à n'importe quelle autre ville dans la communauté ? Justifiez votre réponse à l'aide d'une démonstration formelle.
3. En supposant que les route(s) identifiée(s) à la question 2 sont construites, dressez la liste des plus courts chemins permettant de partir de la capitale vers les autres villes par application de l'algorithme de Dijkstra : vous devez préciser le chemin à parcourir ainsi que sa distance totale.
4. Si on construit une voie à double sens entre Douala et Garoua telle que la distance entre Garoua et Douala soit de 25 km aussi, doit-on définitivement abandonner la voie reliant Maroua à Limbe ? Donnez deux raisons justifiant votre réponse.

Exercice 1 : Calcul des Complexités (6 pts)

Soit la récurrence :

$$ T(n) = 3T\left(\frac{n}{2}\right) + n $$

Méthode de l’arbre récursif :

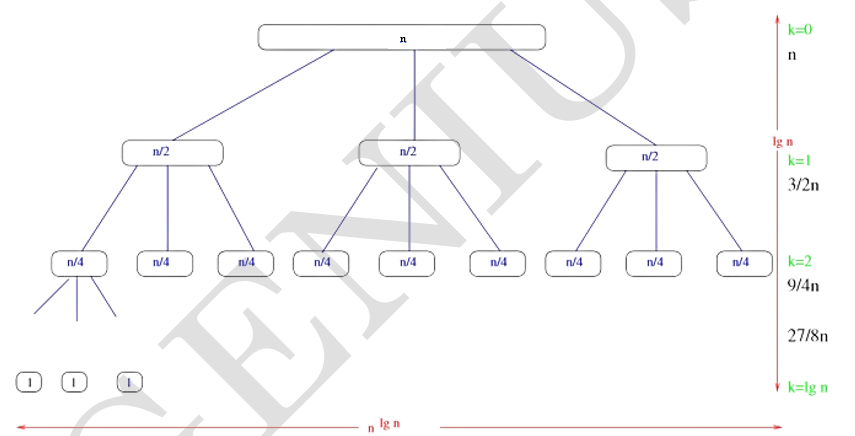
$$ T(n) = \sum_{i=0}^{h} n \left(\frac{3}{2}\right)^i = n \left(\frac{3}{2}\right)^h = n \left(\frac{3}{2}\right)^{\log_2 n} = n \frac{3^{\log_2 n}}{2^{\log_2 n}} = n \frac{3^{\log_2 n}}{n} = 3^{\log_2 n} = O\left(n \left(\frac{3}{2}\right)^h\right) = O\left(n^{\log_2 3}\right) $$

Méthode par substitution :

$$ T(n) = 3T\left(\frac{n}{2}\right) + n $$ $$ T\left(\frac{n}{2}\right) = 3T\left(\frac{(n/2)}{2}\right) + \frac{n}{2} = 3T\left(\frac{n}{4}\right) + \frac{n}{2} $$ $$ T(n) = 3T(n/2) + n = 3\left[3T(n/4) + \frac{n}{2}\right] + n = 9T(n/4) + \frac{3n}{2} + n $$ $$ T(n/4) = 3T\left(\frac{n/4}{2}\right) + \frac{n}{4} = 9\left[3T(n/8) + \frac{n}{4}\right] + \frac{3n}{2} + n $$ $$ = 27T(n/8) + \frac{9n}{4} + \frac{3n}{2} + n $$

En continuant de cette manière :

$$ 3^K T\left(\frac{n}{2^K}\right) + n\left[\frac{3}{2} + \left(\frac{3}{2}\right)^2 + \cdots + \left(\frac{3}{2}\right)^{K-1}\right] $$

Nous savons que :

$$ 2^K = n \quad \Rightarrow \quad \log_2 K = \log_2 n $$ $$ 3^{\log n} T\left(1\right) + n\left(\frac{3^K}{2^K}\right) $$ $$ 3^{\log n} T(1) + n\left[\frac{3^{\log_2 n}}{n^{\log_2 2}}\right] $$ $$ = n^{\log_2 3} + n\left[\frac{n^{\log_2 3}}{n^{\log_2 2}}\right] = 2n^{\log_2 3} = O(n^{\log_2 3}) $$

Obtenue à la question 1.

Je prends un exemple pour expliquer un peu :

Si nous prenons un tableau T de taille n = 4, et l’élément à rechercher est x = 100 :

1 -3 42 19

Le pire des cas est celui où l’élément x n’existe pas dans la liste et par conséquent nous allons (itérer n fois) effectuer n tests pour le rechercher alors qu’il n’est pas présent dans le tableau, cette complexité est de l’ordre O(n).

Facile : Si la liste est triée, nous pouvons appliquer la recherche dichotomique, recherche qui ne s’effectue que sur une liste (tableau) triée d’éléments. La complexité est ainsi améliorée (on se rappelle que la recherche dichotomique utilise le paradigme diviser pour mieux régner : DPR) nous obtenons donc une complexité dont l’ordre de grandeur est de l’ordre O(log n).

Rappels : O(log n) < O(n)

Classe de complexités

Démontrer que, pour tout n ≥ 1, le nombre total de multiplications effectuées par un appel à exporapide(a, n) est inférieur ou égal à 2 + 2 \lfloor \log_2 n \rfloor.

On va procéder par récurrence forte sur n ≥ 1. On fixe a et pour tout n ≥ 1, notons P(n) la propriété "un appel à exporapide(a, n) effectue au plus 2 + 2 \lfloor \log_2 n \rfloor multiplications".

Initialisation : exporapide(a, 1) effectue deux multiplications, et 2 = 2 + 2 \lfloor \log_2 1 \rfloor.

Hérédité : On suppose que P(k) est vraie pour tout k ≤ n−1 et on va prouver que P(n+1) est vraie. On distingue alors deux cas :

• Si n est pair : le nombre total de multiplications effectuées par exporapide(a, n) est égal à 1 plus le nombre de multiplications effectuées par exporapide(a, n/2). Par hypothèse de récurrence, le nombre total est inférieur ou égal à 1 + 2 + 2 \lfloor \log_2 (n/2) \rfloor. Mais \log_2(n/2) = \log_2(n) - 1 et donc le nombre d'appels est majoré par 1 + 2 + 2 \lfloor \log_2(n) \rfloor - 2 ≤ 2 + 2 \lfloor \log_2(n) \rfloor.
• Si n est impair : dans ce cas, exporapide(a, n) effectue deux multiplications et autant de multiplications que exporapide(a, (n-1)/2). Par hypothèse de récurrence, le nombre total de multiplications est donc majoré par 2 + 2 + 2 \lfloor \log_2((n−1)/2) \rfloor ≤ 4 + 2 \lfloor \log_2(n−1) \rfloor - 2 ≤ 2 + 2 \lfloor \log_2(n) \rfloor.

Dans tous les cas, on a prouvé que P(n) est vérifiée. Conclusion : par le principe de récurrence forte, P(n) est vrai pour tout n ≥ 1.

Exercice 2 : Algorithmes Gloutons (3 pts)

Formalisme de L’Algorithme Glouton :

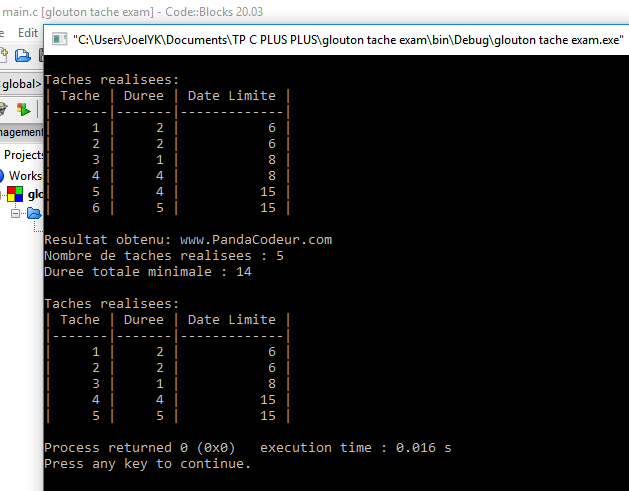
Preuve : j’ai implémenté un code en C pour pouvoir vérifier ma solution gloutonne. Code : GitHub

avec mes Tâches :

Tâche 1 : { durée : 5 , dateL : 15 }
Tâche 2 : { durée : 2 , dateL : 6 }
Tâche 3 : { durée : 4 , dateL : 15 }
Tâche 4 : { durée : 4 , dateL : 8 }
Tâche 5 : { durée : 1 , dateL : 8 }
Tâche 6 : { durée : 5 , dateL : 6 }

Exercice 3 : Algorithme de Prim (2 pts)

1) Appliquons l’algorithme de Prim :

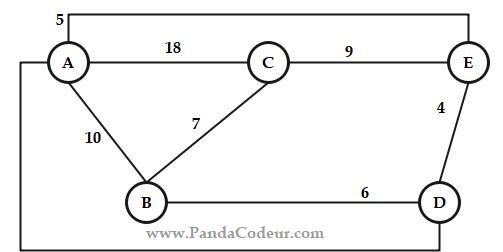
Ensuite :

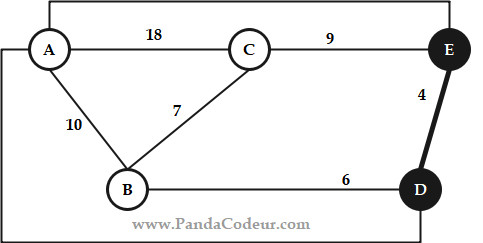
Ensuite :

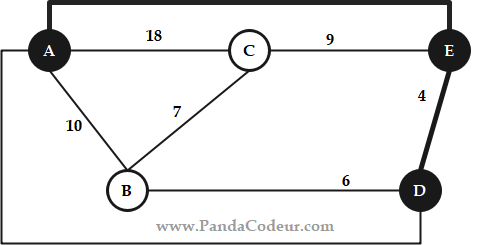Ensuite :

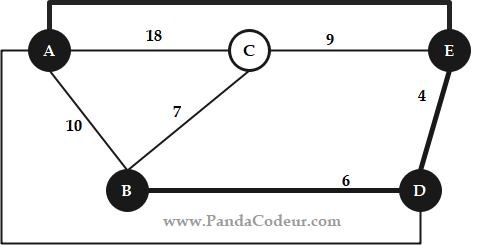Ensuite :

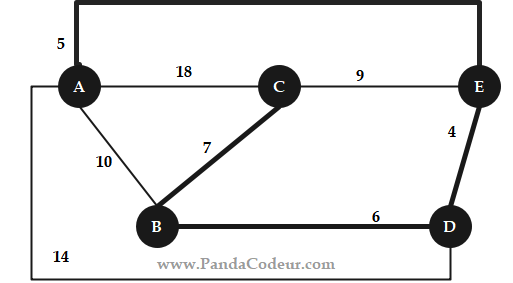
Enfin : L’arbre couvrant minimal, de coût = 22

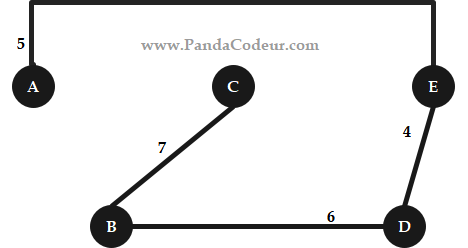
Exercice 4 : Graphes (9 pts)

Nous avons le Graphe (G) suivant modélisant le problème donné :

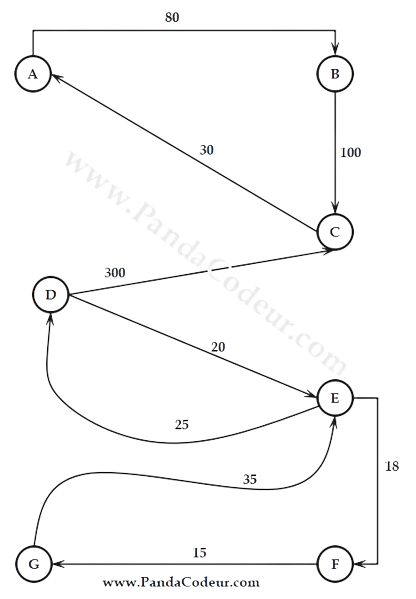
Soit G=(S,A) ou S ={A,B,C,D,E,F,G}

Non, il n'est pas possible de se rendre dans n'importe quelle autre ville en étant dans n'importe quelle ville. On constate que ce graphe n'est pas connexe, c'est-à-dire qu'il existe des sommets qui ne sont pas reliés entre eux par un chemin. Par exemple, il n'existe pas de chemin entre B et D, ni entre C et F ON peut s’arrêter ici avec la démonstration. Où :  on peut le prouver en utilisant le théorème suivant : un graphe est connexe si et seulement si pour tout couple de sommets, il existe un chemin les reliant. Si le graphe est connexe, alors par définition, il existe un chemin entre tout couple de sommets. Par l'absurde : supposons qu'il existe un graphe G celui de note modélisation tel que pour tout couple de sommets, il existe un chemin les reliant, mais que G ne soit pas connexe. Alors, il existe au moins deux composantes connexes distinctes C1 et C2 dans G, c'est-à-dire deux sous-graphes maximaux connexes de G. Soient u un sommet de C1 et v un sommet de C2. Par hypothèse, il existe un chemin P entre u et v dans G. Mais alors, P contient au moins une arête e qui relie un sommet de C1 à un sommet de C2. Or, cela contredit la maximalité de C1 et C2, car on pourrait ajouter e et le sommet de C2 à C1, ou e et le sommet de C1 à C2, pour obtenir un sous-graphe connexe plus grand. On a donc une contradiction, ce qui prouve que G est connexe. En appliquant ce théorème au graphe du tableau, on voit qu'il n'est pas connexe, car il n'existe pas de chemin entre certains sommets.

2) Nous pouvons relier C et G

Explications : Pour permettre des déplacements entre toutes les villes, des routes supplémentaires doivent être

Construites pour connecter les différentes composantes fortement connectées du graphe. Le graphe se divise principalement en deux grandes composantes fortement connectées :

1. La première composante inclut :

Newtown(A), Schooltown(B), et Sexytown(C).

2. La seconde composante inclut :

Greattown(F), Lifetown(E), Naturetown(D), et Oldtown(G).

Pour assurer une connectivité complète, des routes doivent être ajoutées pour connecter ces deux composantes. Cependant, le tableau et Graphe inclut des routes redondantes et ne tient pas compte de l'optimisation ou de la nécessité réelle.

2. A partir de la questions 2) vous élaborer un Graphe Connexe. Faut choisir un sommet arbitraire cela dépend de vous :

4) A partir de la Questions 3)  et 2 )