Examen Cryptographie Sujet 09

EXAMEN CRYPTOGRAPHIE, cryptologie | SUJET 09

Examen corrige cryptographie

Examinateur : Mr JoëlYK

Questions de Cours (05 pts)

1. Que signifie les concepts de confusion et de diffusion en cryptographie ?
2. Que signifie un cryptosystème inconditionnellement sûr ? Donner un exemple s’il en existe.
3. Faites une comparaison entre les systèmes symétriques et les systèmes asymétrique selon au moins 5 critères.
4. Qu’est ce qu’une substitution de polygrammes ?
5. A l’aide d’un schéma, expliquez le fonctionnement d’un chiffre par flux en faisant la distinction entre les modes synchrone et asynchrone.

Exercice 1 : chiffrement RSA (6pts)

Bob et Alice utilisent pour communiquer le système de chiffrement RSA. Bob publie sa clé publique (N, e) = (5183, 11). Alice lui transmet le message chiffré c = 3. Sachant que Bob a l’habitude de prendre pour nombres premiers (p, q) des nombres premiers jumeaux c’est-à-dire tels que q = p + 2, calculez p et q.

1. Calculez l’exposant de déchiffrement d.
2. Que devez-vous calculer pour obtenir le clair x ? (on ne demande pas dans cette question d’exécuter le calcul).
3. Maintenant vous allez calculer x en utilisant le théorème des restes chinois.
4. Calculez une relation de Bézout entre p et q.
5. Calculez 3^d mod p et 3^d mod q en utilisant le petit théorème de Fermat.
6. Utilisez le théorème chinois pour déduire des questions précédentes la valeur de x.

exercice 02 : force brute et analyse des frequences (09pts)

Partie A :  Force brute

1. Déchiffrer le message (chiffré avec le système par décalage) par force brute. « JBCRCLQRWCRVNBJENBWRWN ».
2. Décoder le message : « RGNEIDVGPEWXTRAPHHXFJT » sachant qu'il a été créé par un chiffrement par décalage.

Partie B : Analyse de fréquence
L'analyse des fréquences d'apparition des lettres dans un message codé montre que ceux sont les lettres H et F les plus fréquentes dans ce message. Dans un texte En français, les
lettres les plus rencontrées sont dans l’ordre : E S A I N T R U L O D C P M V Q G F H B X J Y Z K W. Avec les fréquences (souvent proches et dépendant de l’échantillon utilisé) :

Voici la méthode d’attaque : dans le texte crypté, on cherche la lettre qui apparaît le plus, et si le texte est assez long cela devrait être le chiffrement du E, la lettre qui apparaît ensuite dans l’étude des fréquences devrait être le chiffrement du S, puis le chiffrement du A... On obtient des morceaux de texte clair sous la forme d’un texte à trous et il faut ensuite deviner les lettres manquantes. Sachant que le message est en français, codé en utilisant le chiffrement par décalage sur les 26 lettres de l'alphabet, déterminer la clef et déchiffrer le début du message : « LHLZ HFQ BC HFFPZ WH YOUPFH MUPZH »

Questions de cours   
1) La confusion correspond à une volonté de rendre la relation entre la clé de chiffrement et le texte chiffré la plus complexe possible. La diffusion est une propriété où la redondance statistique dans un texte clair est dissipée dans les statistiques du texte chiffré.
2) Un système de chiffrement est dit inconditionnellement sûr si un attaquant est incapable de le casser même en disposant d’une capacité infinie de calcul. Le masque jetable est le seul exemple à ce jour.
3) Comparaison entre les systèmes symétriques et les systèmes asymétrique selon au moins 5 critères :

4) Une substitution de polygrammes est une substitution qu’on opère sur des blocs (groupes) de caractères (ou lettres) au lieu d’opérer sur un seul caractère (une lettre).
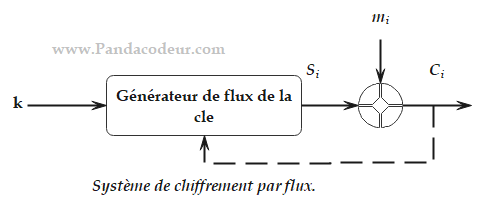
5) Un chiffre par flux est un système symétrique et se présente souvent comme l’illustre le schéma suivant. Un générateur de nombres pseudo-aléatoires ayant comme germe la clé secrète K, produit une séquence binaire si à laquelle on mélange (souvent un XOR bit à bit) la séquence binaire du message clair mi. Le résultat du mélange est une séquence binaire ci qui représente le message chiffré. Si le flus de la clé si est indépendant de la sortie ci, le système est qualifié de synchrone, sinon (un feedback de ci) il est asynchrone

Exercice 1 : rsa

1. Puisque q = p + 2, on a N = p(p + 2) = p² + 2p donc (p + 1)² = N + 1 = 5184 = 72²
Finalement, p = 71 et q = 73.
2. L’exposant de déchiffrement d est l’inverse de e = 11 modulo (p−1)(q−1) = 70∗72 = 5040.
On exécute l’algorithme d’Euclide étendu :
5040  1   0
11      0    1      458      5040 = 458 ∗ 11 + 2
2       1   −458 2          11 = 5 ∗ 2 + 1
1    −5     2291

d’où la relation de Bezout 1 = 5040 ∗ (−5) + 11 ∗ 2291 donc d = 2291.
3) x = 3²²⁹¹ mod 5183
4.

73   1   0
71   0   1   1        73 = 71 + 2
2     1 −1  35        71 = 35 ∗ 2 + 1
1  −35   36
D’où 73 ∗ (−35) + 71 ∗ 36 = 1.

5. Comme 2291 = 70 ∗ 32 + 51, 3²²⁹¹ = 3⁵¹ mod 71. Ensuite on calcule 3⁵¹ mod 71 par exponentiation rapide. 51 s’écrit en binaire 110011.
  1
1 3
1 27
0 19
0 6
1 37
1 60

Donc 3⁵¹ = 60 mod 71.

De même, comme 2291 = 72 ∗ 31 + 59, 3²²⁹¹ = 3⁵⁹ mod 73.
1
1 3
1 27
1 70
0 9
1 24
1 49

Donc 3⁵⁹ = 49 mod 73.

6. Comme x = 60 mod 71 et x = 49 mod 73, par le théorème Chinois, on a x = 60 ∗ 73 ∗ (−35) + 49 ∗ 71 ∗ 36 = 3042 mod 5183.

EXERCICE 2 :

Si vous avez trouvé les examenscorrigés en Cryptographie de Mr JoëlYk intéressants et utiles, pourquoi ne pas les partager avec d'autres personnes qui pourraient également en bénéficier ? Partagez ce lien sur les réseaux sociaux ou envoyez-le à vos amis et collègues. Vous pourriez aider quelqu'un à améliorer ses compétences en programmation ou à trouver des solutions à des problèmes complexes. N'oubliez pas que la connaissance doit être partagée pour grandir. Merci pour votre soutien et votre partage !

Contact WhatsApp : +237 658395978 | Réaliser Par Joël_Yk

 encore plus d'examen corriges ici !!!