1. Accueil
  2. EXAMEN PANDACODEUR
  3. Examen Electronique numerique
  4. Examen Electronique Numerique 01

Examen Electronique Numerique 01

Examen electronique, sujet corrige electronique numerique.

 Exercice 1 : Application du cours 4 points

  1. On considère le schéma à contact suivant :
    Schema contact pandacodeur

    1. Transformer ce schéma en équation logique.                                                                        0,5pt
    2. En supposant que le produit des variables A et B l’unité (AB=1)
  2. Donner la table de vérité permettant de commander la lampe S1 que nous noterons S. on prendra le reste des variables dans l’ordre C, D, E.                                                  1pt
  3. Donner l’équation simplifiée de S 1.5pt

        1.3. Donner l’expression de S1 en fonction de S puis déduire l’équation logique de S1 globale en fonction de toutes les variables. C’est – à- dire S1 = f(A, B, C, D, E).                                                    1pt

SOLUTION :

Exercice 1 : Application du Cours /4pts

On considère le schéma à contact suivant :

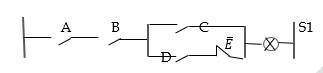
Schema contact pandacodeur

1.1. L’équation logique est :

S1 = A · B · (C + D·E̅)

a) En supposant que AB = 1

C D E S
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1

b) Équation simplifiée de S1 :

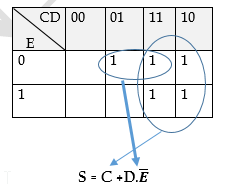Table de karnaugh
S = C + D·E̅
Donc S1 = A·B·S
Équation globale de S1 :
S1 = A · B · (C + D·E̅)
Exercice 2 : Circuits Combinatoire /6pts

2.1) Table de Vérité :

a b c d F1 F2
0 0 0 0 1 0
0 0 0 1 0 1
0 0 1 0 0 1
0 0 1 1 0 1
0 1 0 0 1 0
0 1 0 1 1 0
0 1 1 0 1 0
0 1 1 1 0 1
1 0 0 0 1 0
1 0 0 1 1 0
1 0 1 0 1 0
1 0 1 1 0 1
1 1 0 0 1 0
1 1 0 1 1 0
1 1 1 0 1 0
1 1 1 1 1 0

2.2) Expression des sorties sous forme de somme de produits (Première Forme Canonique)

F1 =  a̅b̅c̅d̅ +  a̅bc̅d̅ + a̅bc̅d + ab̅c̅d̅ + ab̅c̅d + a̅bcd̅  + ab̅cd̅ + abc̅d̅ + abc̅d + abcd̅ + abcd
F2 =  a̅b̅c̅d + a̅b̅cd̅ + a̅b̅cd + a̅bcd + ab̅cd

2.3) Simplification graphique des expressions de F1 et F2 :

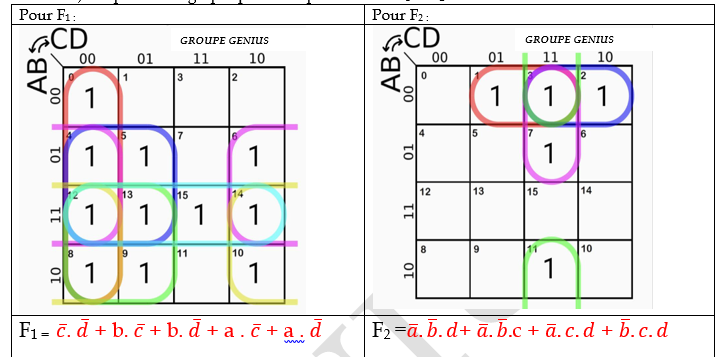Simplification algebrique pandacodeur
Pour F1 :                      Pour F2 :
F1 =  c̅. d̅ + b. c̅ + b. d̅ + a . c̅ + a . d̅     F2 =a̅.b̅.d+ a̅.b̅.c + a̅.c.d + b̅.c.d
Problème : Comparateur - Transcodeur /10 pts

Synthèse du Comparateur 1 Bit :

Table de vérité :

xi yi S I E
0 0 0 0 1
0 1 0 1 0
1 0 1 0 0
1 1 0 0 1

Équations des Sorties :

S = xi y̅i         ,       I = x̅i yi
E = x̅iy̅i + xiyi   =  (xi ⊕ yi)̅

Logigramme :

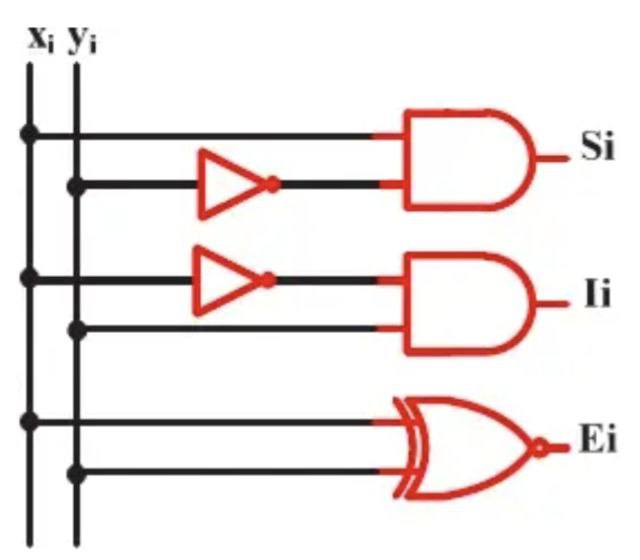
Logigramme xiyi

Compléter le Tableau suivant :

On réalise le comparateur de deux nombres binaires à trois bits X=X2X1X0 et Y=Y2Y1Y0, à base de trois comparateurs 1 bit comme l'indique la figure ci-contre. Pour cela, on détermine les expressions des sorties S, I et E en fonctions des sorties des 3 comparateurs 1 bit S2, I2, E2, S1, I1, E1, S0, et E0.

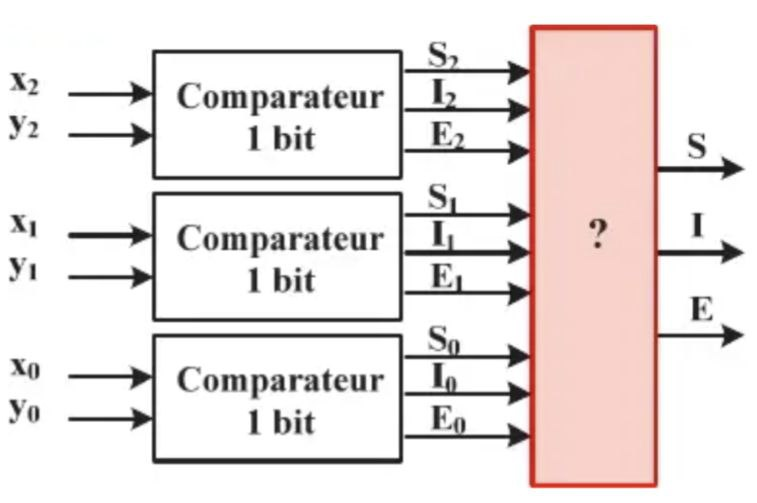
Comparateur schema

a. Expressions logiques des sorties S, I, E :

X>Y (S=1) si :
X2>Y2 (S2 =1) 
Ou X2=Y2 (E2=1) et X1>Y1 (S1=1)
Ou X2=Y2 (E2=1) et X1=Y1 (E1=1) et X0>Y0 (S1=1)
D’où S = S2 + E2S1 + E2E1S0

X22 (I2=1)
Ou X2=Y2 (E2=1) et X11 (I1=1)
Ou X2=Y2 (E2=1) et X1=Y1 (E1=1) et X00 (I0= 1)
D’où S = I2 + E2I1 + E2E1I0

X=Y (E=1) si :
X2=Y2 (E2=1) et X1=Y1 (E1=1) et X0=Y0 (E0=1)
D’où E = E2E1E0

b. Logigramme :

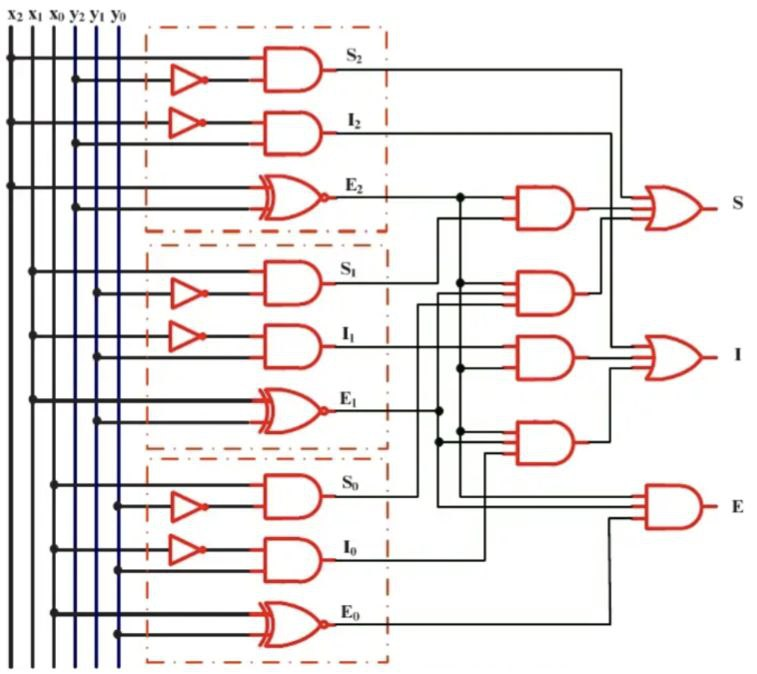
Logigrame comparateur

Etude du Transcodeur :

Table de vérité :

S I E a b c d e f g
0 0 1 1 0 0 1 1 1 1
0 1 0 0 0 0 0 1 1 0
1 0 0 1 0 1 1 0 1 1

D’après la table de vérité on déduit les équations des différentes sorties :

a = b = g = I̅ 
b = 0 
c = S 
e = S̅ 
f = 1

Schéma interne du Transcodeur :

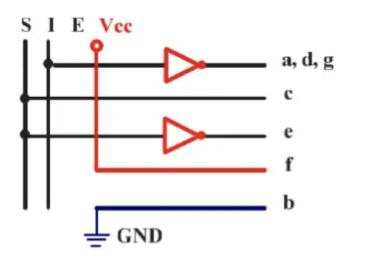
Schema interne transcodeur

Remarque : On peut établir la table de vérité du transcodeur de la façon suivante où chaque ꬾ représente un état indéterminé de la sortie.

S I E a b c d e f g
0 0 0 ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ
0 0 1 1 0 0 1 1 1 1
0 1 0 0 0 0 0 1 1 0
0 1 1 ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ
1 0 0 1 0 1 1 0 1 1
1 0 1 ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ
1 1 0 ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ
1 1 1 ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ ꬾ

D’où les équations simplifient des sorties a et c match avec ce qu’on a trouvé plus haut :

a = I̅ 
c = S

Si vous avez trouvé cet Examen en Electronique numerique  de Mr JoëlYk intéressants et utiles, pourquoi ne pas les partager avec d'autres personnes qui pourraient également en bénéficier ? Partagez ce lien sur les réseaux sociaux ou envoyez-le à vos amis et collègues. Vous pourriez aider quelqu'un à améliorer ses compétences en programmation ou à trouver des solutions à des problèmes complexes. N'oubliez pas que la connaissance doit être partagée pour grandir. Merci pour votre soutien et votre partage !

Contact WhatsApp : +237 652027193 | Réaliser Par Joël_Yk

Partager via :

  • 1 vote. Moyenne 1 sur 5.

Ajouter un commentaire

Anti-spam