CORRIGE EXAMEN FOUILLE DE DONNEE :
EXERCICE 1 :
EXERCICE 2 :
1)
2) Seuil de support =33.34% ---> le seuil est d'au moins 2 transactions. Application de la méthode de l'algo Apriori
| k | k-itemsets candidats et leur support | k-itemsets fréquents |
|---|---|---|
| 1 | Peanuts(4), Lemon(2), Grape(2), Orange(3), Apple(4) | Peanuts, Lemon, Grape, Orange, Apple |
| 2 | {Peanuts, Lemon}(2), |
{Peanuts, Lemon}, {Peanuts, Orange}, {Peanuts, Apple}, {Orange, Apple} |
| 3 | {Peanuts, Orange, Apple}(2) | {Peanuts, Orange, Apple} |
| 4 | { } |
|
Notez que {Peanuts, Lemon, Orange} et {Peanuts, Lemon, Apple} ne sont pas des candidats lorsque k=3 car leurs sous-ensembles {Lemon, Orange} et {Lemon, Apple} ne sont pas fréquents. Notez également qu'en général, il n'est pas nécessaire d'aller jusqu'à k=4 car la transaction la plus longue ne contient que 3 éléments.
2) Tous les ensembles d'items fréquents : {Peanuts}, {Lemon}, {Grape}, {Orange}, {Apple}, {Peanuts, Lemon}, {Peanuts, Orange}, {Peanuts, Apple}, {Orange, Apple}, {Peanuts, Orange, Apple}.
Règles d'association :
{Peanuts, Lemon} générerait : Peanuts ----> Lemon (2/6=0.33, 2/4=0.5) et Lemon ----> Peanuts (2/6=0.33, 2/2=1) ;
{Peanuts, Orange} générerait : Peanuts ----> Orange (0.33, 0.5) et Orange ----> Peanuts (2/6=0.33, 2/3=0.66) ;
{Peanuts, Apple} générerait : Peanuts ----> Apple (0.33, 0.5) et Apple ----> Peanuts (2/6=0.33, 2/4=0.5) ;
{Orange, Apple} générerait : Orange ----> Apple (3/6=0.5, 3/3=1) et Apple ----> Orange (3/6=0.5, 3/4=0.75) ;
{Peanuts, Orange, Apple} générerait : Peanuts ----> Orange ^ Apple (2/6=0.33, 2/4=0.5), Orange ----> Apple ^ Peanuts (2/6=0.33, 2/3=0.66), Apple ----> Orange ^ Peanuts (2/6=0.33, 2/4=0.5), Peanuts ^ Orange ----> Apple (2/6=0.33, 2/2=1), Peanuts ^ Apple ----> Orange (2/6=0.33, 2/2=1) et Orange ^ Apple ----> Peanuts (2/6=0.33, 2/3=0.66).
3) Avec un seuil de confiance fixé à 60%, les règles d'association fortes sont (triées par confiance) :
1. Orange ----> Apple (0.5, 1)
2. Lemon ----> Peanuts (0.33, 1)
3. Peanuts ^ Orange ----> Apple (0.33, 1)
4. Peanuts ^ Apple ----> Orange (0.33, 1)
5. Apple ----> Orange (0.5, 0.75)
6. Orange ----> Peanuts (0.33, 0.66)
7. Orange ----> Apple ^ Peanuts (0.33, 0.66)
8. Orange ^ Apple ----> Peanuts (0.33, 0.66).
EXERCICE 03 :
A) SVM
1) On peut s'attendre à ce que les vecteurs de support restent généralement les mêmes lorsque l'on passe d'un noyau linéaire à des noyaux polynomiaux d'ordre supérieur. Réponse : Faux ( Il n'y a aucune garantie que les vecteurs de support restent les mêmes. Les vecteurs caractéristiques correspondant aux noyaux polynomiaux sont des fonctions non linéaires des vecteurs d'entrée d'origine et les points d'appui pour la séparation de la marge maximale dans l'espace caractéristique peuvent donc être très différents. )
2) Les limites de décision à marge maximale construites par les machines à vecteurs de support présentent l'erreur de généralisation la plus faible de tous les classifiers linéaires. Réponse : Faux ( L'hyperplan à marge maximale est souvent un choix raisonnable, mais il n'est en aucun cas optimal dans tous les cas. )
3) Toute limite de décision obtenue à partir d'un modèle génératif avec des distributions gaussiennes conditionnelles par classe pourrait en principe être reproduite avec un SVM et un noyau polynomial de degré inférieur ou égal à trois. Réponse : Vrai (Un noyau polynomial de degré deux suffit à représenter toute frontière de décision quadratique telle que celle du modèle génératif en question).
4) Les valeurs des marges obtenues par deux noyaux différents K1(x,x0) et K2(x,x0) sur le même ensemble d'apprentissage ne nous indiquent pas quel classifier sera le plus performant sur l'ensemble de test. Réponse : Vrai ( Il faut normaliser la marge pour qu'elle soit significative. Par exemple, une simple mise à l'échelle des vecteurs de caractéristiques conduirait à une marge plus importante. Toutefois, une telle mise à l'échelle ne modifie pas la limite de décision et la marge plus importante ne peut donc pas nous informer directement sur la généralisation. )
B) RESEAU DE NEURONES
Soit A et B deux variables booléennes.
1) Concevoir un réseau de neurones à deux entrées permettant d’implémenter la fonction booléenne A∧¬B.
Solution : La conception d'un réseau de neurones à deux entrées pour implémenter la fonction booléenne A∧¬B, consiste à trouver les poids (w0,w1,w2) qui définissent un hyperplan de séparation entre les exemples positifs et négatifs. Dans ce cas, les exemples positifs correspondent à A∧¬B=1, et les exemples négatifs correspondent à A∧¬B=−1.
L'équation générale pour le perceptron est donnée par y=f(w0+w1⋅A+w2⋅B), où f est une fonction d'activation, souvent la fonction échelon (step function) dans le contexte des fonctions booléennes.
Dans ce cas, les valeurs possibles pour A et B sont 1 et -1. Pour les exemples positifs (A∧¬B=1), la sortie du perceptron doit être positive, donc (w0+w1⋅A+w2⋅B)>0. Pour les exemples négatifs (A∧¬B=−1), la sortie du perceptron doit être négative, donc w0+w1⋅A+w2⋅B<0
| A | B | A∧¬B | w0+w1⋅A+w2⋅B | y (perceptron) |
|---|---|---|---|---|
| -1 | -1 | -1 | -1 | -1 |
| -1 | 1 | -1 | -1 | -1 |
| 1 | -1 | 1 | 1 | 1 |
| 1 | 1 | -1 | -1 | -1 |
En utilisant les exemples donnés dans le tableau (A, B, y) :
- (−1,−1,−1): w0+w1⋅(−1)+w2⋅(−1)<0
- (−1,1,−1): w0+w1⋅(−1)+w2⋅1<0
- (1,−1,1): w0+w1⋅1+w2⋅(−1)>0
- (1,1,−1): w0+w1⋅1+w2⋅1<0
En simplifiant ces inégalités, on peut obtenir :
- −w0−w1−w2<0
- −w0+w1−w2<0
- w0+w1−w2>0
- w0+w1+w2<0
Une des surfaces de décision correctes (n’importe quelle droite séparant le point positif des points négatifs serait correcte) est affichée dans la figure suivante :
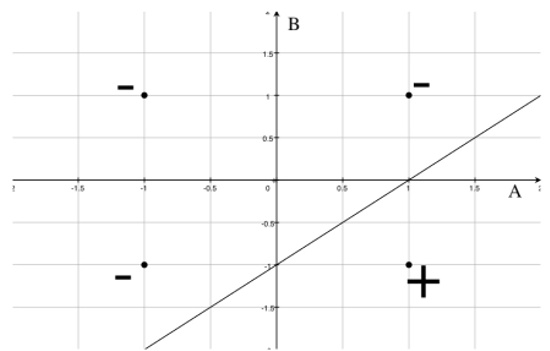
La droite traversant l'axe A en 1 et l'axe B en –1 {A (1,0) et B (0,-1)}. Donc l'équation de la droite est :
(A-0)/(1-0)=(B-(-1))/(0-(-1)) =>A=B+1=>1-A+B=0
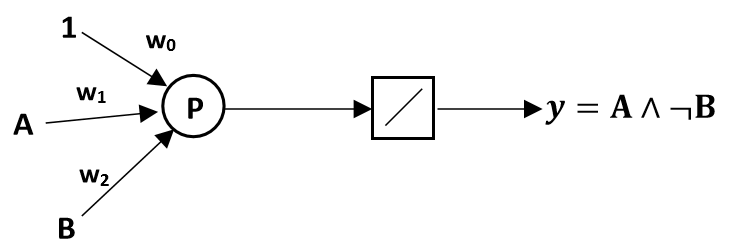
Les valeurs possibles pour les poids w0, w1 et w2 sont 1 et -1. En utilisant ces valeurs, la sortie du perceptron pour A = 1, B = -1 est positive. Par conséquent, nous pouvons conclure que w0=-1, w1=1, w2=-1.
2) Concevoir un réseau de neurones à deux couches implémentant la fonction booléenne A XOR B.
Solution : Le perceptron demandé a 3 entrées : A, B et la constante 1. Les valeurs de A et B sont 1 (vrai) ou −1 (faux). Le tableau suivant décrit la sortie y du perceptron :
| A | B | ¬A∧¬B | y (perceptron) |
|---|---|---|---|
| -1 | -1 | 1 | 1 |
| -1 | 1 | -1 | -1 |
| 1 | -1 | -1 | -1 |
| 1 | 1 | -1 | -1 |
Une des surfaces de décision correctes (n’importe quelle droite séparant les points positifs des points négatifs serait correcte) est affichée dans la figure suivante :
La droite traversant l'axe A en −1 et l'axe B en −1. Donc l'équation de la droite est :
(A-0)/(-1-0)=(B-(-1))/(0-(-1))=>A=-B-1=>1+A+B=0
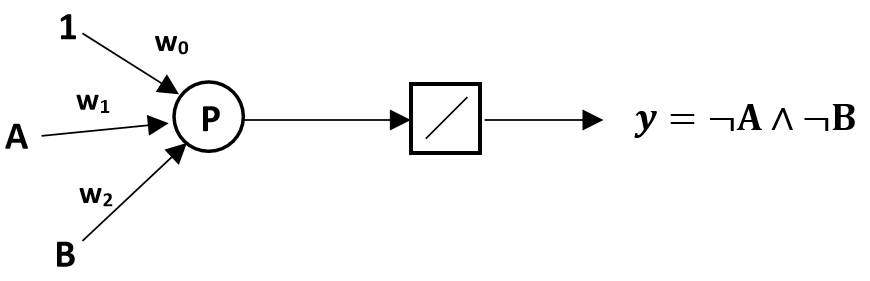Les valeurs possibles pour les poids w0, w1 et w2 sont 1 et -1. En utilisant ces valeurs, la sortie du perceptron pour A = -1, B = -1 est positive. Par conséquent, nous pouvons conclure que w0=-0,7, w1=-0,5, w2=-0,5.
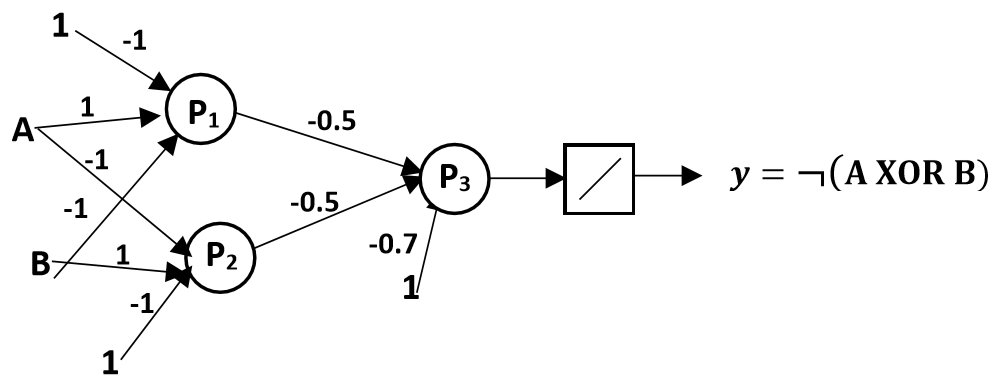
3) En déduire : ¬(A XOR B) ne peut pas être calculé par un perceptron unique, nous devons donc construire un réseau à deux couches de perceptrons. La structure du réseau peut être dérivée par :
¬(A XOR B) = ¬((A∧¬B)∨(¬A∧B)) = ¬(A∧¬B)∧¬(¬A∧B)
- Exprimer ¬(A XOR B) en fonction des composantes logiques :
- Définir les perceptrons P1 et P2 pour (A∧¬B) et (¬A∧B)
- Combiner les sorties de P1 et P2 dans P3 qui implémente ¬f(P1)∧¬f(P2)
La structure du réseau à deux couches peut être définie comme suit :
Télécharger L'exercice Sous Forme de PDF
Ajouter un commentaire