Examen Fouille de donnée Sujet 2

examen data mining

Exercice 1 : CLASSIFICATION PAR ARBRE DE décision 05pts

Une banque dispose des informations suivantes sur un ensemble de ses clients :

Questions :

1. Quelle est l'entropie de la population ?
2. Pour la construction de l'arbre de décision, utilisez-vous l'attribut numéro de client ? Pourquoi ?
3. Lors de la construction de l'arbre de décision, quel est l'attribut à tester à la racine de l'arbre ?
4. Construisez l'arbre de décision complet.
5. Quel est le taux d'erreur de cet arbre estimé sur l'ensemble des clients 1 à 8 ?
6. Donnez un intervalle de valeurs pour l'erreur réelle en utilisant une confiance de 90%.

On se donne les 4 clients suivants :

7) Comment chacun de ces clients est-il classé avec l'arbre de décision que vous avez proposé dans la question 4?

Pour ces 4 clients, on apprend par ailleurs que les clients 9 et 10 gèrent leur compte par Internet, et que les clients 11 et 12 ne le font pas.

8) Quel est le taux d'erreur estimé sur les clients 9, 10, 11 et 12? Combien y a-t-il de faux positifs et de faux négatifs?

Exercice 2 : classification avec la technique des k-means 05pts

Utilisez l'algorithme du K-means et la distance euclidienne pour regrouper les 8 exemples suivants en 3 clusters : A1(2,10), A2(2,5), A3(8,4), A4(5,8), A5(7,5), A6(6,4), A7(1,2), A8(4,9).

La matrice de distance basée sur la distance euclidienne est fournie ci-dessous :

On considère comme centre de classe à l'initialisation les points A1, A4 et A7.

1) Déroulez  une itération de l'algorithme de K-means pour ces données et cette initialisation     et donnez :

- Les nouveaux clusters ;

- Les centres de chaque cluster ;

- Faites une représentation graphique montrant les points d'étude, les clusters et les centres de clusters.

  2) Combien d’itérations supplémentaire sont-elles nécessaires pour converger ?

            Dessinez les résultats de chaque itération nécessaire.

Exercice 3 : RÉSEAUX DE NEURONES 05pts

 Soit A et B deux variables booléennes.

1. Concevoir un réseau de neurones à deux entrées permettant d’implémenter la fonction booléenne A∧¬B.
2. Concevoir un réseau de neurones à deux couches implémentant la fonction booléenne A XOR B.
3. En déduire un réseau de neurones implémentant la fonction booléenne : ¬(A XOR B) sachant que : ¬(A XOR B) = ¬((A∧¬B)∨(¬A∧B)) = ¬(A∧¬B)∧¬(¬A∧B)

Exercice 4 : Generation de règles d'association 05pts 

Soit X la base de transactions contenant un ensemble de transactions décrivant des achats de produits dans l'ensemble  {A, B, C, D, E}.

1. Montrer que l'union de deux itemsets fréquents n'est pas toujours fréquent ;

2. Générer les règles d'association avec minConf = 1 pour les données de la base X ;

3. Considérons seulement l'ensemble {A, B, C} ; Trouver l'ensemble de règles qui permettent de prédire l'achat de deux produits tout en améliorant la prédiction par rapport à la mesure statistique induite par la base de données ;

4. Répéter la même question pour trouver l'ensemble de règles qui permettent de prédire l'achat d'un produit.

EXERCICE 1 :

EXERCICE 2 :

On considère comme centre de classe à l'initialisation les points A1, A4 et A7.

1. Déroulez une itération de l'algorithme de K-means pour ces données et cette. initialisation et donnez:

d(a,b) désigne la distance euclidienne entre ? et ?. Elle est obtenue directement à partir de la matrice de distance ou calculée comme suit :

d(a,b)=  √ (x_b-x_a)²-(y_b-y_a)²

CENTRE1 = A1 = (2,10), CENTRE2 = A4 = (5,8), CENTRE3 = A7 = (1,2) :

L'algorithme de K-means attribue chaque point au cluster associé au centre de classe le plus proche. Voici comment les nouveaux clusters sont formés après une itération :

• Cluster 1 : {A1}
  • A1 reste dans le cluster 1 car il est déjà le centre de classe pour ce cluster.
• Cluster 2 : {A3, A4, A5, A6, A8}
  • A3 est plus proche de CENTRE2 (A4) que des autres centres, donc il est attribué au Cluster 2.
  • A4 reste dans le Cluster 2 car il est déjà le centre de classe pour ce cluster.
  • A5 est plus proche de CENTRE2 (A4) que des autres centres, donc il est attribué au Cluster 2.
  • A6 est plus proche de CENTRE2 (A4) que des autres centres, donc il est attribué au Cluster 2.
  • A8 est plus proche de CENTRE2 (A4) que des autres centres, donc il est attribué au Cluster 2.
• Cluster 3 : {A2, A7}
  • A2 est plus proche de CENTRE3 (A7) que des autres centres, donc il est attribué au Cluster 3.
  • A7 reste dans le Cluster 3 car il est déjà le centre de classe pour ce cluster.

Les Nouveaux clusters sont :

1 : {A1}

2 : {A3, A4, A5, A6, A8}

3 : {A2, A7}

b) Centres des nouveaux clusters.

Pour calculer les nouveaux centres de classe (C1, C2, C3) après la première itération de l'algorithme K-means, vous prenez la moyenne des coordonnées de tous les points appartenant à chaque cluster respectif.

Nouveaux centres de classe :

• C1 : (2,10)
  • Cluster 1 ne contient qu'un seul point, qui est A1. Donc, le nouveau centre C1 est simplement les coordonnées de A1.
• C2 : ((8 + 5 + 7 + 6 + 4)/5, (4 + 8 + 5 + 4 + 9)/5) = (6 ,6)
  • Cluster 2 contient les points {?3, ?4, ?5, ?6, ?8}. Les nouvelles coordonnées du centre C2 sont la moyenne des coordonnées de ces points.
  • Nouvelle coordonnée x de C2 : (8 + 5 + 7 + 6 + 4) / 5 = 6
  • Nouvelle coordonnée y de C2 : (4 + 8 + 5 + 4 + 9) / 5 = 6
• C3 : ((2 + 1)/2, (5 + 2)/2) = (1.5,3.5)
  • Cluster 3 contient les points {?2, ?7}. Les nouvelles coordonnées du centre C3 sont la moyenne des coordonnées de ces points.
  • Nouvelle coordonnée x de C3 : (2 + 1) / 2 = 1.5
  • Nouvelle coordonnée y de C3 : (5 + 2) / 2 = 3.5

En résumé, les nouveaux centres de classe sont :

• C1 = (2,10)
• C2 = (6,6)
• C3 = (1.5,3.5)

C1 = (2,10),C2 = ((8 + 5 + 7 + 6 + 4)/5,(4 + 8 + 5 + 4 + 9)/5) = (6 ,6),C3 = ((2 + 1)/2,(5 + 2)/2) = (1.5,3.5)

c) Faites une représentation graphique montrant les points d’études, les clusters et les centres des clusters :

Pour ce faits nous allons représentez ces éléments sur le graphique, pour  visualiser la distribution des points dans chaque cluster et l'emplacement des centres des clusters. Nous allons faires que les couleurs ou symboles utilisés pour les clusters sont distincts pour une meilleure compréhension visuelle. Dessinons un espace 10 sur 10 avec tous les 8 points et montrons les clusters apres la première it et les nouveaux centroïdes.

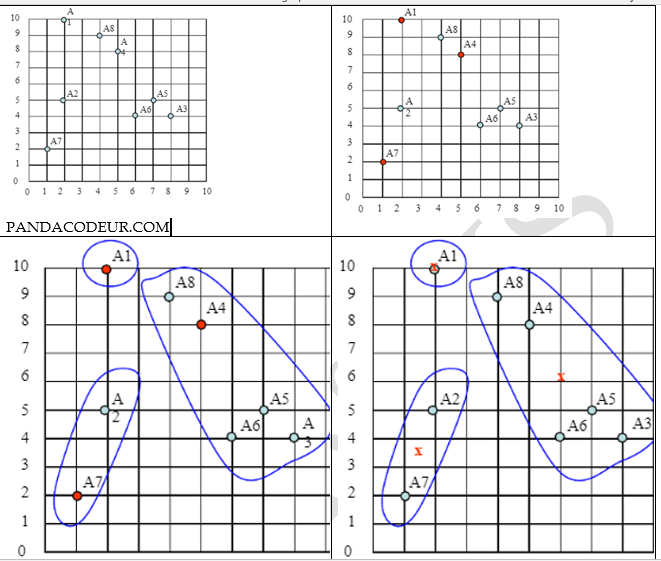
Cette représentation graphique nous permettra de voir comment les points sont regroupés en fonction des itérations successives de l'algorithme K-means et comment les centres des clusters évoluent.

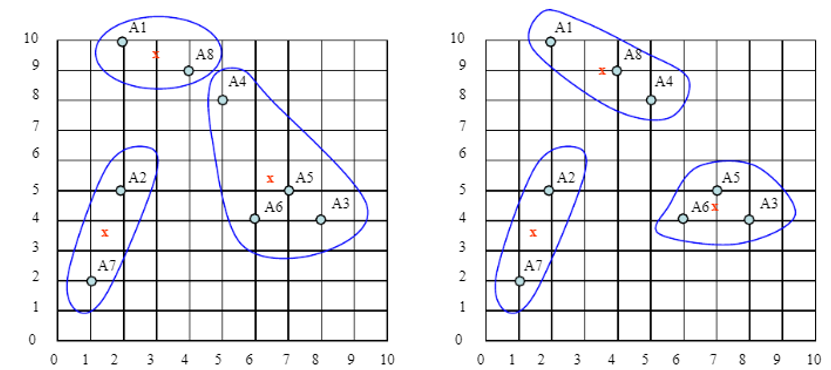
1. Combien d'itérations supplémentaires sont nécessaires pour converger ? Dessinez le résultat de chaque itération :

1 : {A1,A8},2 : {A3,A4,A5,A6},3 : {A2,A7} avec les centres A1 = (3,9.5),A2 = (6.5 ,5,25) et A3 = (1,5,3,5). 

Après la 3ème itération, les résultats seraient : 

1 : {A1,A4,A8},2 : {A3,A5,A6},3 : {A2,A7} de centres A1= (3.66,9),A2 = ( 7,4.33) ET C3 = (1.5,3.5).

Le processus que j’ai implémentée se décompose comme suit :

1. Après la première itération, les nouveaux centres de classe sont calculés en prenant la moyenne des coordonnées des points dans chaque cluster.

2. Les points sont ensuite réattribués aux clusters en fonction de leur proximité aux nouveaux centres de classe.

3. Le processus se répète jusqu'à ce que les centres de classe ne changent plus entre deux itérations successives.

4. La convergence est atteinte lorsque les centres de classe ne changent plus significativement, et les points restent dans les mêmes clusters.

Dans ce cas, après la deuxième itération, les clusters et les centres de classe évoluent.

2ème Itération :

- Nouveaux centres de classe :

  - C1 = (3,9.5)

  - C2 = (6.5,5.25)

  - C3 = (1.5,3.5)

- Nouveaux clusters :

  - Cluster 1 : {A1, A8}

  - Cluster 2 : {A3, A4, A5, A6}

  - Cluster 3 : {A2, A7}

Enfin, après la troisième itération, les clusters convergent vers une configuration stable. Ces résultats montrent que deux itérations supplémentaires sont nécessaires pour que l'algorithme K-means converge dans ce cas spécifique.

3ème Itération :

- Nouveaux centres de classe :

  - A1 = (3.66,9)

  - A2 = (7,4.33)

  - A3 = (1.5,3.5)

- Nouveaux clusters :

  - Cluster 1 : {A1, A4, A8}

  - Cluster 2 : {A3, A5, A6}

  - Cluster 3 : {A2, A7}

EXERCICE 03 :

Soit A et B deux variables booléennes.

1) Concevoir un réseau de neurones à deux entrées permettant d’implémenter la fonction booléenne A∧¬B.

Solution : La conception d'un réseau de neurones à deux entrées pour implémenter la fonction booléenne A∧¬B, consiste à trouver les poids (w0,w1,w2) qui définissent un hyperplan de séparation entre les exemples positifs et négatifs. Dans ce cas, les exemples positifs correspondent à A∧¬B=1, et les exemples négatifs correspondent à A∧¬B=−1.

L'équation générale pour le perceptron est donnée par y=f(w0+w1⋅A+w2⋅B), où f est une fonction d'activation, souvent la fonction échelon (step function) dans le contexte des fonctions booléennes.

Dans ce cas, les valeurs possibles pour A et B sont 1 et -1. Pour les exemples positifs (A∧¬B=1), la sortie du perceptron doit être positive, donc (w0+w1⋅A+w2⋅B)>0. Pour les exemples négatifs (A∧¬B=−1), la sortie du perceptron doit être négative, donc w0+w1⋅A+w2⋅B<0

ABA∧¬Bw0+w1⋅A+w2⋅By (perceptron)

-1-1-1-1-1

-11-1-1-1

1-1111

11-1-1-1

En utilisant les exemples donnés dans le tableau (A, B, y) :

(−1,−1,−1): w0+w1⋅(−1)+w2⋅(−1)<0

(−1,1,−1): w0+w1⋅(−1)+w2⋅1<0

(1,−1,1): w0+w1⋅1+w2⋅(−1)>0

(1,1,−1): w0+w1⋅1+w2⋅1<0

En simplifiant ces inégalités, on peut obtenir :

−w0−w1−w2<0

−w0+w1−w2<0

w0+w1−w2>0

w0+w1+w2<0

Une des surfaces de décision correctes (n’importe quelle droite séparant le point positif des points négatifs serait correcte) est affichée dans la figure suivante :

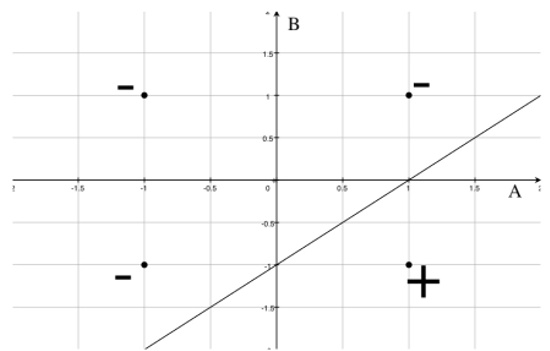
La droite traversant l'axe A en 1 et l'axe B en –1 {A (1,0) et B (0,-1)}. Donc l'équation de la droite est :

(A-0)/(1-0)=(B-(-1))/(0-(-1)) =>A=B+1=>1-A+B=0

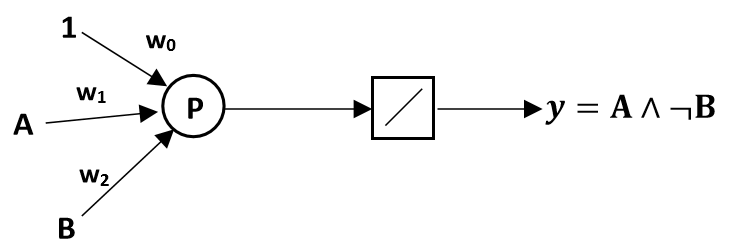
Les valeurs possibles pour les poids w0, w1 et w2 sont 1 et -1. En utilisant ces valeurs, la sortie du perceptron pour A = 1, B = -1 est positive. Par conséquent, nous pouvons conclure que w0=-1, w1=1, w2=-1.

2) Concevoir un réseau de neurones à deux couches implémentant la fonction booléenne A XOR B.

Solution : Le perceptron demandé a 3 entrées : A, B et la constante 1. Les valeurs de A et B sont 1 (vrai) ou −1 (faux). Le tableau suivant décrit la sortie y du perceptron :

AB¬A∧¬By (perceptron)

-1-111

-11-1-1

1-1-1-1

11-1-1

Une des surfaces de décision correctes (n’importe quelle droite séparant les points positifs des points négatifs serait correcte) est affichée dans la figure suivante :

La droite traversant l'axe A en −1 et l'axe B en −1. Donc l'équation de la droite est :

(A-0)/(-1-0)=(B-(-1))/(0-(-1))=>A=-B-1=>1+A+B=0

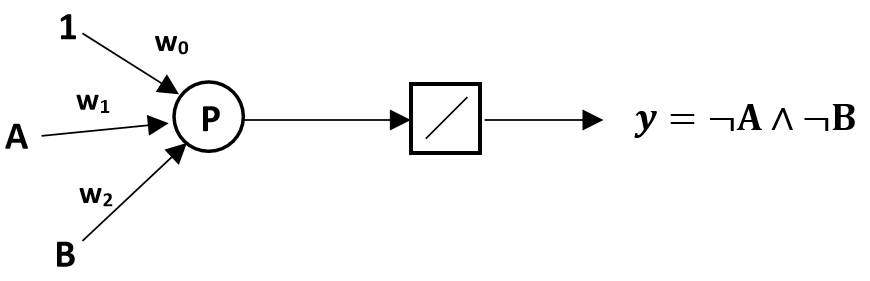Les valeurs possibles pour les poids w0, w1 et w2 sont 1 et -1. En utilisant ces valeurs, la sortie du perceptron pour A = -1, B = -1 est positive. Par conséquent, nous pouvons conclure que w0=-0,7, w1=-0,5, w2=-0,5.

3) En déduire : ¬(A XOR B) ne peut pas être calculé par un perceptron unique, nous devons donc construire un réseau à deux couches de perceptrons. La structure du réseau peut être dérivée par :

¬(A XOR B) = ¬((A∧¬B)∨(¬A∧B)) = ¬(A∧¬B)∧¬(¬A∧B)

Exprimer ¬(A XOR B) en fonction des composantes logiques :

Définir les perceptrons P1 et P2 pour (A∧¬B) et (¬A∧B)

Combiner les sorties de P1 et P2 dans P3 qui implémente ¬f(P1)∧¬f(P2)

La structure du réseau à deux couches peut être définie comme suit :

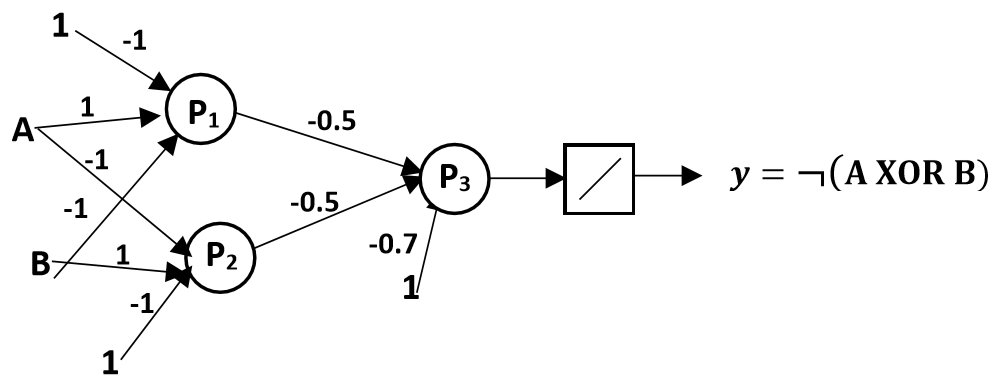
EXERCICE 04 :

Encore plus d'examenEncore plus d'examen corrige ici !!!