Correction.
1 - Algorithme :
#include <stdio.h>
void apparierBoulonsEtEcrous(int boulons[], int ecrous[], int n) {
for (int i = 0; i < n; i++) {
int boulonCourant = boulons[i];
for (int j = 0; j < n; j++) {
if (ecrous[j] == boulonCourant) {
printf("Le boulon %d correspond à l'écrou %d\n", boulonCourant, boulonCourant);
break;
}
}
}
}
int main() {
int n;
printf("Entrez le nombre de boulons/écrous : ");
scanf("%d", &n);
int boulons[n], ecrous[n];
printf("Entrez les diamètres des %d boulons : ", n);
for (int i = 0; i < n; i++) {
scanf("%d", &boulons[i]);
}
printf("Entrez les diamètres des %d écrous : ", n);
for (int i = 0; i < n; i++) {
scanf("%d", &ecrous[i]);
}
apparierBoulonsEtEcrous(boulons, ecrous, n);
return 0;
}
Explication de l'Algorithme :
- Cet algorithme utilise une approche de force brute pour appareiller chaque boulon avec son écrou correspondant.
- La fonction apparierBoulonsEtEcrous prend deux tableaux d'entiers (boulons et ecrous) ainsi que la taille n.
- Dans la boucle externe, chaque boulon est pris un par un et comparé avec tous les écrous dans la boucle interne.
- Lorsqu'un boulon et un écrou correspondent (c'est-à-dire qu'ils ont le même diamètre), l'algorithme affiche un message indiquant que le boulon correspond à l'écrou.
Note : Pour appareiller les boulons et les écrous, il suffit de prendre un boulon arbitrairement, de le tester avec tous les écrous.On trouve alors le bon en au plus n tests et il suffit alors de recommencer avec tous les autres boulons.On obtient donc le résultat en au plus n(n−1) 2 = O(n^2) tests.
2 - Le plus petit écrou et son boulon Le principe est de numéroter les boulons et les écrous de 1 à n, de manière arbitraire, et de faire progresser des compteurs (par exemple i et j) pour marquer le minimun courant dans l’une des catégories, et la structure en cours de test dans l’autre.
début
while (i≤n) && (j ≤n) do
si i=j=n alors sortir de la boucle ;
si ecrou.i = boulon.j alors s’en souvenir et faire i := i+1;
si ecrou.i < boulon.j alors j := j +1; min = ecrou;
si ecrou.i > boulon.j alors i := i+1; min = boulon;
fin.
A la fin de cette boucle,
– si min=écrou, l’écrou i est le plus petit.
– si min=boulon, le boulon j est le plus petit. Et dans les deux cas, on sait déjà quel est l’élémentquicorrespond:eneffet,lecompteurdel’autrecatégorievautn+1(oundansun cas spécial),et on a donc déjà rencontré le minimum. la seule raison possible pour laquelle il n’a pas été conservé est donc qu’il ait été testé avec l’autre minimum. Pour le cas spécial ou i=j=n, le dernier test est inutile : en effet, on sait que l’un des deux, est minimum, et que une fois le boulon minimum atteind, j reste fixe : d’où le boulon n est minimum, et son homologue a soit déjà été trouvé, soit est l’écrou restant. Cette boucle effectue donc au plus 2∗n−2 tests.
3 - Algorithme d’appareillage des écrous et de leur boulon
On note f(T) le nombre de feuilles de l’arbre et h(T) sa hauteur.
Si T est un arbre ternaire h(T)≥[log3f(T)]. Par induction sur la hauteur de T :
– Pour h(T) = 0 l’arbre à une feuille donc on a bien h(T)≥[log3f(T)].
– Pour h(T) > 0 un arbre ternaire a trois fils, le fils gauche fg, le fils central fc, et le fils droit fd de hauteur inférieur à h(T)−1.On suppose que h(T) ≥[log3f(T)] est vrai pour h(T) ≤ k k étant fixé on veut démontrer que cette propriété est vrai aussi pour h(T) = k +1. Les feuilles d’un arbre sont aussi celles de ses fils. Donc
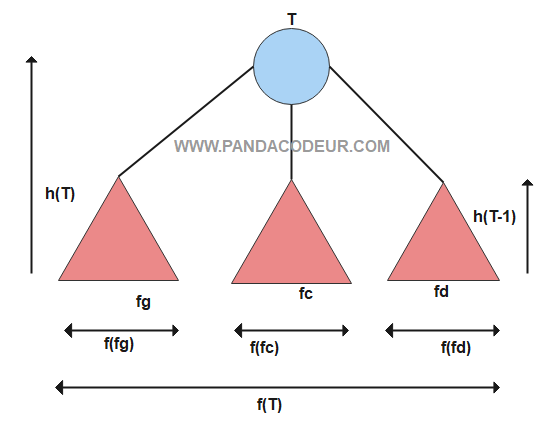
f(T) = f(fd)+f(fg)+f(fd)
de plus :
h(T)≤h(fd)+1
h(T)≤h(fg)+1
h(T)≤h(fc)+1
or par induction comme h(T) = k +1, h(fg)≤k, h(fg)≤k,et h(fg)≤k
on a : k = h(fc)≤[log3f(fc)]
h(fd)≤[log3f(fd)]
h(fg)≤[log3f(fg)] Donc f(fc),f(fg),f(fd)≤3^k or : f(T) = f(fc)+f(fg)+f(fd) donc : f(T)≤3×3^k = 3^(k+1)
D’ où on en déduit que : h(T)≥log3f(T) Il y a !n agencements boulons-écrous possibles donc l’arbre de décision, qui est ternaire a pour hauteur : log3!n∼nlog3n, donc la complexité dans le pire cas de l’algo est de : Ω(n×logn).


