EXERCICE 01 : Systèmes logiques combinatoires

EXERCICE  CORRIGE ELECTRONIQUE NUMERIQUE :

1) Établir la table de vérité, puis donner la forme canonique de la fonction logique suivante :

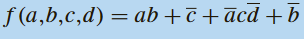
2) Établir la table de vérité, puis donner la forme canonique de la fonction logique suivante :

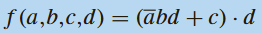
3) Déterminer l’expression de la fonction logique représentée par le schéma de la figure ci-contre :

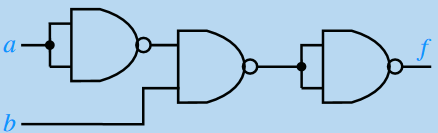
4) Déterminer l’expression de la fonction logique représentée par le schéma de la figure ci-contre :

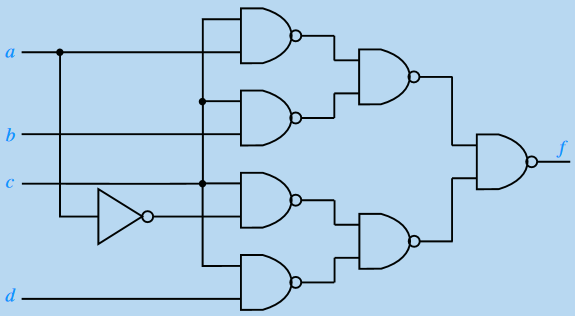
5) On considère la fonction logique définie par :

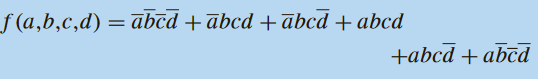
Établir la forme minimale de cette fonction logique et proposer son schéma en n’utilisant que des portes NAND à deux entrées.

6) On considère la fonction logique définie par :

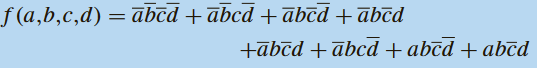
Établir la forme minimale de cette fonction logique et proposer son schéma en n’utilisant que des portes NOR à deux entrées.

7) Proposer un circuit réalisant la fonction OU-Exclusif de deux variables, en n’utilisant que des portes NAND à deux entrées.

8) On considère le montage de la figure ci-dessous. Établir l’expression de la fonction f et, proposer, le cas échéant, un nouveau montage plus économique.

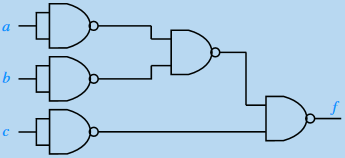
9) On considère 2 nombres binaires de 2 bits chacun (susceptibles de varier, par conséquent entre 00 et 11), notés : x = (ab)₂ et y = (cd)₂ On souhaite construire un dispositif à l’entrée duquel on injecte ces deux nombres et fournissant, à sa sortie, une fonction f définie par f = 1 ⇐⇒ x < y (voir figure ci-dessous) :

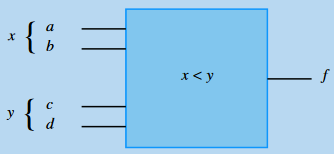
Établir la forme minimale de la fonction logique permettant de réaliser cette comparaison et implanter le dispositif en n’utilisant que des portes NAND à deux entrées. Comment peut-on rapidement concevoir, à partir de ce dispositif, un système permettant de réaliser la fonction définie par : g = 1 ⇐⇒ x
>=  y .